Problem 1: This question considers the Bayesian estimators for the population mean and variance.

(a) Let \({{y}_{i}}\) iid N( \(\mu \), \({{\sigma }^{2}}\) ) for i = 1, ..., n. Show that the ML estimator of \(\mu \) and \({{\sigma }^{2}}\) are, respectively,

(b) We know that \({{\hat{\sigma }}^{2}}\) always tends to underestimate \({{\sigma }^{2}}\), particularly when the sample size n

is small. Now we try to run a simulation to assess the Bayesian estimation of \({{\sigma }^{2}}\).

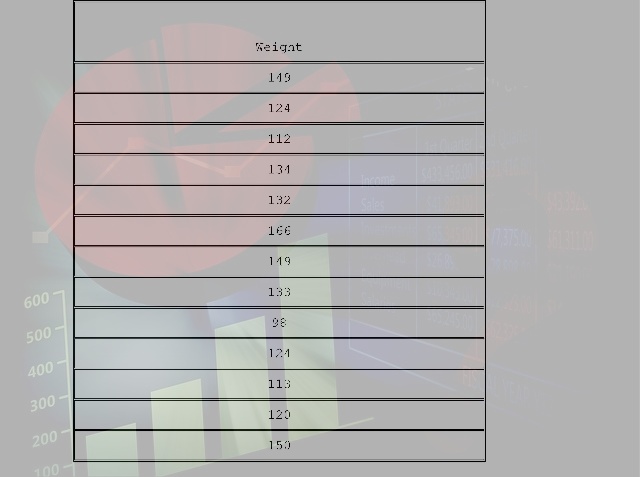
(1) Generate n = 10 observations from N(10, 2²) distribution. Display your MATLAB

code and the data.

(2) From this simulated data set, what is the ML estimate of t and \({{\sigma }^{2}}\) ?

Problem 2: We have learned how to fit a simple logistic regression model by the ML method. This

question considers fitting a logistic regression by the Bayesian method. Suppose binary valued independent responses \({{y}_{i}}\), i = 1, ...,n, adopt

\[E\left( {{y}_{i}} \right)=\frac{{{e}^{{{\beta }_{0}}+{{\beta }_{1}}{{x}_{i}}}}}{1+{{e}^{{{\beta }_{0}}+{{\beta }_{1}}{{x}_{i}}}}}\]

and we want to estimate \({{\beta }_{0}}\) and \({{\beta }_{1}}\), from observations on y and x. and in particular, the

posterior mean estimator of \({{\beta }_{0}}\) and \({{\beta }_{1}}\). The prior distribution for \({{\beta }_{0}}\) and \({{\beta }_{1}}\) are assumed to be:

\[{{\beta }_{0}}\tilde{\ }Unif\left( {{{\hat{\beta }}}_{0}}-2,{{{\hat{\beta }}}_{0}}+2 \right)\,\text{and }{{\beta }_{1}}\tilde{\ }Unif\left( {{{\hat{\beta }}}_{1}}-0.2,{{{\hat{\beta }}}_{1}}+0.2 \right)\,\]

where \({{\hat{\beta }}_{0}}\) and \({{\hat{\beta }}_{1}}\) represent the ML estimate of \({{\beta }_{0}}\) and \({{\beta }_{1}}\) respectively. Data on y and x

variables are given in the file "radio.dat" which can be obtained from the unit web page.,

Price: $20.95

Solution: The downloadable solution consists of 5 pages, and 336 words
Deliverable: Word Document and pdf