(Solution) We have the following decision variables: - #80190
Problem 1:
We have the following decision variables:
\[\begin{aligned} & {{x}_{1}}=\text{Amount of space for supermarket} \\ & {{x}_{2}}=\text{Amount of space Discount Store} \\ & {{x}_{3}}=\text{Amount of space for fabric store} \\ & {{x}_{4}}=\text{Amount of space for women }\!\!'\!\!\text{ s specialty store} \\ & {{x}_{5}}=\text{Amount of space for men }\!\!'\!\!\text{ s specialty store} \\ & {{x}_{6}}=\text{Amount of space for hardware store} \\ & {{x}_{7}}=\text{Amount of space for drugstore} \\ & {{x}_{8}}=\text{Amount of space for gift store} \\ & {{x}_{9}}=\text{Amount of space for bakery} \\ & {{x}_{10}}=\text{Amount of space for ice cream stand} \\ & {{x}_{11}}=\text{Amount of space for music store} \\ & {{x}_{12}}=\text{Amount of space for barber shop} \\\end{aligned}\]
All these variables are measured in thousands of square feet.
We have the following linear problem:
\[\begin{aligned} & Maximize\,\,\,\,\,52{{x}_{1}}+67{{x}_{2}}+23{{x}_{3}}+42{{x}_{4}}+41{{x}_{5}}+45{{x}_{6}}+37{{x}_{7}}+29{{x}_{8}}+39{{x}_{9}}+30{{x}_{10}}+39{{x}_{11}}+24{{x}_{12}} \\ & s.t. \\ & {{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}}+{{x}_{8}}+{{x}_{9}}+{{x}_{10}}+{{x}_{11}}+{{x}_{12}}\le 45 \\ & 10\le {{x}_{1}}\le 20 \\ & 10\le {{x}_{2}}\le 20 \\ & {{x}_{3}}\le 0.9 \\ & {{x}_{4}}\le 3 \\ & {{x}_{5}}\le 2 \\ & {{x}_{6}}\le 4 \\ & {{x}_{7}}\le 1.6 \\ & {{x}_{8}}\le 3 \\ & {{x}_{9}}\le 1.3 \\ & {{x}_{10}}\le 1.5 \\ & {{x}_{11}}\le 1.5 \\ & {{x}_{12}}\le 1 \\ & {{x}_{3}}+{{x}_{4}}+{{x}_{5}}\ge 3 \\ & {{x}_{6}}+{{x}_{7}}\ge 3 \\ & {{x}_{8}}+{{x}_{9}}\ge 3 \\ & \,10{{x}_{1}}+13{{x}_{2}}+12{{x}_{3}}+8{{x}_{4}}+7{{x}_{5}}+7{{x}_{6}}+9{{x}_{7}}+9{{x}_{8}}+11{{x}_{9}}+10{{x}_{10}}+7{{x}_{11}}+11{{x}_{12}}\le 450 \\ & 3.2{{x}_{1}}+4.1{{x}_{2}}+3{{x}_{3}}+3.2{{x}_{4}}+3.2{{x}_{5}}+3{{x}_{6}}+3.1{{x}_{7}}+2.5{{x}_{8}}+2.4{{x}_{9}}+2.6{{x}_{10}}+2.3{{x}_{11}}+3{{x}_{12}}\ge 125 \\ & {{x}_{i}}\ge 0 \\\end{aligned}\]
Linearity seems to be appropriate in this case. Linearity doesn’t capture though one subtlety of this model, which is the fact that Vista will get 6% of the sales if they go beyond a certain level.
(b) The option should be exercised for several reasons: First, the extra capital required is $296,000, which accounts for extra $96,000 over the land price. The net present value of after tax flows will be $23/ square foot. Since the project would bring extra 6,000 square-foot, the expected extra flow would be at least \(6,000\times 23=\\)138,000$. We have to consider that the extra 6,000 ft2 are not enough for stores of the Group A.
On the other hand, the extra cost will be increased by $29,000 a year. The guaranteed rent for stores that are not from Group A is $2.83 / ft2 in average. So, the extra rent revenues would be in average \(6,000\times 2.83=\\)16,980$, which doesn’t cover the extra $29,000. Nevertheless, the overall guaranteed rent is in average $2.97/ ft2, so the original 45,000 ft2 would imply \(45,000\times 2.97=\\)133,500$, which helps to offset the extra fixed cost. So, balancing all the facts, the present value of the extra flow look promising and the Option should be taken.
Note: To be precise, we should solve an LP problem with a new variable y, which is 1 or 0, depending if the option is taken or not. The problem becomes:
\(\begin{aligned}
& Maximize\,\,\,\,\,52{{x}_{1}}+67{{x}_{2}}+23{{x}_{3}}+42{{x}_{4}}+41{{x}_{5}}+45{{x}_{6}}+37{{x}_{7}}+29{{x}_{8}}+39{{x}_{9}}+30{{x}_{10}}+39{{x}_{11}}+24{{x}_{12}}-96 \\ & s.t. \\& {{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}}+{{x}_{8}}+{{x}_{9}}+{{x}_{10}}+{{x}_{11}}+{{x}_{12}}\le 45+6y \\ & 10\le {{x}_{1}}\le 20 \\ & 10\le {{x}_{2}}\le 20 \\ & {{x}_{3}}\le 0.9 \\ & {{x}_{4}}\le 3 \\ & {{x}_{5}}\le 2 \\ & {{x}_{6}}\le 4 \\ & {{x}_{7}}\le 1.6 \\ & {{x}_{8}}\le 3 \\ & {{x}_{9}}\le 1.3 \\ & {{x}_{10}}\le 1.5 \\ & {{x}_{11}}\le 1.5 \\ & {{x}_{12}}\le 1 \\ & {{x}_{3}}+{{x}_{4}}+{{x}_{5}}\ge 3 \\ & {{x}_{6}}+{{x}_{7}}\ge 3 \\ & {{x}_{8}}+{{x}_{9}}\ge 3 \\ & \,10{{x}_{1}}+13{{x}_{2}}+12{{x}_{3}}+8{{x}_{4}}+7{{x}_{5}}+7{{x}_{6}}+9{{x}_{7}}+9{{x}_{8}}+11{{x}_{9}}+10{{x}_{10}}+7{{x}_{11}}+11{{x}_{12}}\le 450+60y \\ & 3.2{{x}_{1}}+4.1{{x}_{2}}+3{{x}_{3}}+3.2{{x}_{4}}+3.2{{x}_{5}}+3{{x}_{6}}+3.1{{x}_{7}}+2.5{{x}_{8}}+2.4{{x}_{9}}+2.6{{x}_{10}}+2.3{{x}_{11}}+3{{x}_{12}}\ge 125+29y \\ & {{x}_{i}}\ge 0,\,y\in \{0,1\} \\ \end{aligned}\)
If this problem is feasible and improves the maximum of the original problem, then the option should be taken
(c) The variable costs of allocating 500 ft2 to an ice cream stand are:
\[10\times 0.5\times 1000=\\] 5,000$
The fixed cost is $154,000 (the original $125,000 plus the $29,000 for taking the Option)
(d) If a hardware stores gets allocated only 25 ft2 that wouldn’t really work, because it doesn’t seem to be enough space. So, maybe the minimum allocations should be rechecked, because 25 ft2 doesn’t seem enough for any kind of store.
(e) Let’s assume that the option is taken, so we have the following problem:
\(\begin{aligned}
& Maximize\,\,\,\,\,52{{x}_{1}}+67{{x}_{2}}+23{{x}_{3}}+42{{x}_{4}}+41{{x}_{5}}+45{{x}_{6}}+37{{x}_{7}}+29{{x}_{8}}+39{{x}_{9}}+30{{x}_{10}}+39{{x}_{11}}+24{{x}_{12}} \\ & s.t. \\& {{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}}+{{x}_{8}}+{{x}_{9}}+{{x}_{10}}+{{x}_{11}}+{{x}_{12}}\le 54 \\ & 10\le {{x}_{1}}\le 20 \\ & 10\le {{x}_{2}}\le 20 \\ & {{x}_{3}}\le 0.9 \\ & {{x}_{4}}\le 3 \\ & {{x}_{5}}\le 2 \\ & {{x}_{6}}\le 4 \\ & {{x}_{7}}\le 1.6 \\ & {{x}_{8}}\le 3 \\ & {{x}_{9}}\le 1.3 \\ & {{x}_{10}}\le 1.5 \\ & {{x}_{11}}\le 1.5 \\ & {{x}_{12}}\le 1 \\ & {{x}_{3}}+{{x}_{4}}+{{x}_{5}}\ge 3 \\ & {{x}_{6}}+{{x}_{7}}\ge 3 \\ & {{x}_{8}}+{{x}_{9}}\ge 3 \\ & \,10{{x}_{1}}+13{{x}_{2}}+12{{x}_{3}}+8{{x}_{4}}+7{{x}_{5}}+7{{x}_{6}}+9{{x}_{7}}+9{{x}_{8}}+11{{x}_{9}}+10{{x}_{10}}+7{{x}_{11}}+11{{x}_{12}}\le 510 \\ & 3.2{{x}_{1}}+4.1{{x}_{2}}+3{{x}_{3}}+3.2{{x}_{4}}+3.2{{x}_{5}}+3{{x}_{6}}+3.1{{x}_{7}}+2.5{{x}_{8}}+2.4{{x}_{9}}+2.6{{x}_{10}}+2.3{{x}_{11}}+3{{x}_{12}}\ge 154 \\ & {{x}_{i}}\ge 0,\,y\in \{0,1\} \\ \end{aligned}\)
- The solution found by LINDO is shown below:
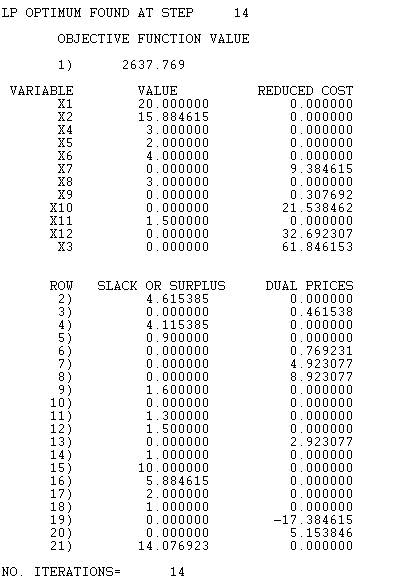
The dual prices for the rows 2) to 13) represent the marginal benefit of an increase in one unit. The binding restrictions of maximum allocation are for x2, x5, x6, x7 and x12
So, the benefit / cost ratio of increasing the maximum allocation is zero, except for
\[\begin{aligned} & B/C\left( {{x}_{2}} \right)=\frac{461.538}{13}=35.5 \\ & B/C\left( {{x}_{5}} \right)=\frac{769}{7}=109.9 \\ & B/C\left( {{x}_{6}} \right)=\frac{4923}{7}=703.3 \\ & B/C\left( {{x}_{7}} \right)=\frac{8923}{9}=991.4 \\ & B/C\left( {{x}_{12}} \right)=\frac{2923}{11}=265.7 \\\end{aligned}\]
Problem 2:
(a) We have the following decision variables:
The number of full time drivers that start their shift on Mondays
The number of full time drivers that start their shift on Tuesdays
The number of full time drivers that start their shift on Wednesdays
The number of full time drivers that start their shift on Thursdays
The number of full time drivers that start their shift on Fridays
The number of full time drivers that start their shift on Saturdays
The number of full time drivers that start their shift on Sundays
The linear programming problem we need to solve can be written as:
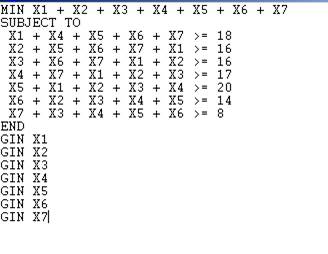
\[\begin{aligned} & Minimize\text{ }{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}} \\ & \text{s}\text{.t}\text{.}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{1}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}}\ge 18 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{2}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}}+{{x}_{1}}\ge 16 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{3}}+{{x}_{6}}+{{x}_{7}}+{{x}_{1}}+{{x}_{2}}\ge 16 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{4}}+{{x}_{7}}+{{x}_{1}}+{{x}_{2}}+{{x}_{3}}\ge 17 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{5}}+{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}\ge 20 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{6}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}\ge 14 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{7}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}\ge 8 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{i}}\text{ are nonnegative integers} \\\end{aligned}\]
We first don’t impose integrality. We have the following model in LINDO:

- The solution found by LINDO is shown below:
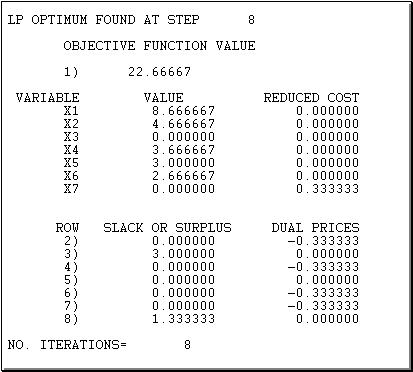
Now we add the integrality condition:
The results are shown below:
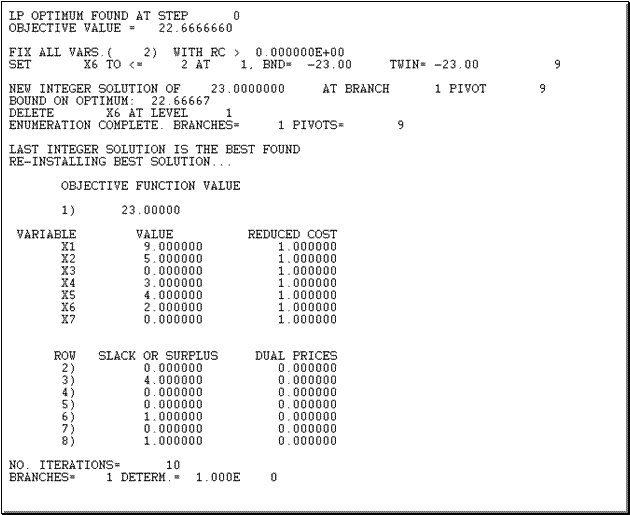
This means that the optimal amount of full time drivers in order to satisfy the demand is 23, of which 9 start their shift on Monday, 5 on Tuesday, none on Wednesday, 3 on Thursday, 4 on Friday, 2 on Saturday and none on Sunday.
(b) We introduce the new set of decision variables:
The number of part-time drivers that start their shift on Mondays
The number of part-time drivers that start their shift on Tuesdays
The number of part-time drivers that start their shift on Wednesdays
The number of part-time drivers that start their shift on Thursdays
The number of part-time drivers that start their shift on Fridays
The number of part-time drivers that start their shift on Saturdays
The number of part-time drivers that start their shift on Sundays
Also, we need variables to consider the possibility of over-time:
The number of overtime drivers on Mondays
The number of overtime drivers on Tuesdays
The number of overtime drivers on Wednesdays
The number of overtime drivers on Thursdays
The number of overtime drivers on Fridays
The number of overtime drivers on Saturdays
The number of overtime drivers on Sundays
The problem becomes
\[\begin{aligned} & Minimize\text{ }{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}} \\ & \text{s}\text{.t}\text{.}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{1}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}}+\frac{{{y}_{1}}}{2}+\frac{{{y}_{4}}}{2}+\frac{{{y}_{5}}}{2}+\frac{{{y}_{6}}}{2}+\frac{{{y}_{7}}}{2}+\frac{{{z}_{1}}}{2}\ge 18 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{2}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}}+{{x}_{1}}+\frac{{{y}_{2}}}{2}+\frac{{{y}_{5}}}{2}+\frac{{{y}_{6}}}{2}+\frac{{{y}_{7}}}{2}+\frac{{{y}_{1}}}{2}+\frac{{{z}_{2}}}{2}\ge 16 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{3}}+{{x}_{6}}+{{x}_{7}}+{{x}_{1}}+{{x}_{2}}+\frac{{{y}_{3}}}{2}+\frac{{{y}_{6}}}{2}+\frac{{{y}_{7}}}{2}+\frac{{{y}_{1}}}{2}+\frac{{{y}_{2}}}{2}+\frac{{{z}_{3}}}{2}\ge 16 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{4}}+{{x}_{7}}+{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+\frac{{{y}_{4}}}{2}+\frac{{{y}_{7}}}{2}+\frac{{{y}_{1}}}{2}+\frac{{{y}_{2}}}{2}+\frac{{{y}_{3}}}{2}+\frac{{{z}_{4}}}{2}\ge 17 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{5}}+{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+\frac{{{y}_{5}}}{2}+\frac{{{y}_{1}}}{2}+\frac{{{y}_{2}}}{2}+\frac{{{y}_{3}}}{2}+\frac{{{y}_{4}}}{2}+\frac{{{z}_{5}}}{2}\ge 20 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{6}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+\frac{{{y}_{6}}}{2}+\frac{{{y}_{2}}}{2}+\frac{{{y}_{3}}}{2}+\frac{{{y}_{4}}}{2}+\frac{{{y}_{5}}}{2}+\frac{{{z}_{6}}}{2}\ge 14 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{7}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+\frac{{{y}_{7}}}{2}+\frac{{{y}_{3}}}{2}+\frac{{{y}_{4}}}{2}+\frac{{{y}_{5}}}{2}+\frac{{{y}_{6}}}{2}+\frac{{{z}_{7}}}{2}\ge 8 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0.35\,\left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}}+{{y}_{4}}+{{y}_{5}}+{{y}_{6}}+{{y}_{7}} \right) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\le 0.25(\frac{1.8}{14}\left( {{z}_{1}}+{{z}_{2}}+{{z}_{3}}+{{z}_{4}}+{{z}_{5}}+{{z}_{6}}+{{z}_{7}} \right)+{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+0.35\left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}}+{{y}_{4}}+{{y}_{5}}+{{y}_{6}}+{{y}_{7}} \right)) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1.8}{14}\left( {{z}_{1}}+{{z}_{2}}+{{z}_{3}}+{{z}_{4}}+{{z}_{5}}+{{z}_{6}}+{{z}_{7}} \right)+0.35\left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}}+{{y}_{4}}+{{y}_{5}}+{{y}_{6}}+{{y}_{7}} \right) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}}\le 21.03 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{2}}+{{x}_{3}}\ge {{z}_{1}} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{3}}+{{x}_{4}}\ge {{z}_{2}} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{4}}+{{x}_{5}}\ge {{z}_{3}} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{5}}+{{x}_{6}}\ge {{z}_{4}} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{6}}+{{x}_{7}}\ge {{z}_{5}} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{7}}+{{x}_{1}}\ge {{z}_{6}} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{1}}+{{x}_{2}}\ge {{z}_{7}} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{i}}\text{,}{{y}_{i}}\text{,}{{z}_{i}}\text{ are nonnegative integers} \\\end{aligned}\]
LINDO took 210,133 iterations. Here’s the output:
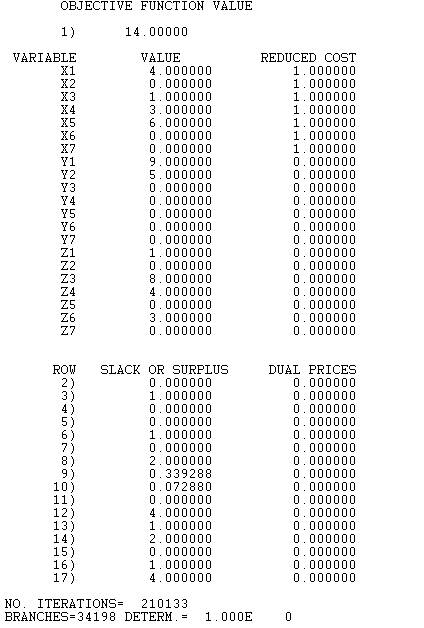
(c) We can assume that the number of part-time workers is at most 11, because of the 25% restriction for part-timers. So adding the restrictions we get:
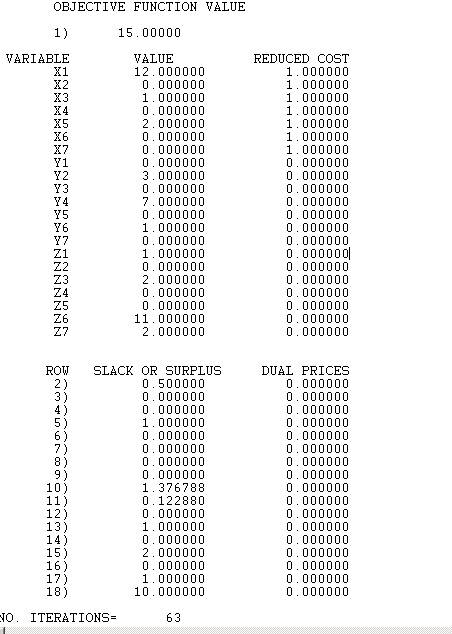
This reduces the number of iterations to 63, but it changes the solution. Now we need 15 full-timers and 11 part-timers
(d) If part time workers were available at the full wage they wouldn’t result in savings
Solution:

Deliverable: Word Document
 and pdf
and pdf

![[Solved] Create scatterplot including the trend line, R2 and the regression equation. - #80029 Statistics](/images/projects/project-80029/statistics-1.jpg)


