Solution: The following four activities were identified as being - #80218

Project Management Problems

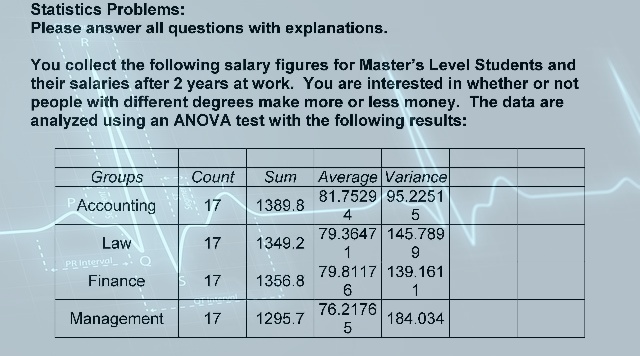
1. The following four activities were identified as being on the critical path of a large project. The project manager wished to reduce the completion time by one week. Which activity should be crashed first.

Activity	Normal Time (weeks)	Normal Cost	Crash Time (weeks)	Crash Cost
A	12	$15,000	6	$18,000
B	8	$17,500	5	$18,850
C	9	$12,200	3	$14,750
D	11	$12,780	7	$14,500

Use the following project network and table to answer the next TWO questions:

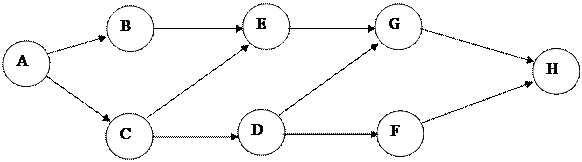Activity Time (days) ES EF LS LF

A 3 0 3 0 3
B 4 3 7 5 9
C 6 3 9 3 9

D 5 9 14 11 16

E 7 9 16 9 16

F 8 14 22 16 24

G 8 16 24 16 24

H 3 24 27 24 27

2. What is the minimum completion time, in days, of the project?

3. For the same network above, what is the latest time the project manager should finish Activity C without delaying the project completion time?

4. Using PERT, the expected completion time for a project is 89 days. The variance of the project completion is 49. What is the probability of completing the project between 82 and 110 days?

Given the following project data,

Activity	Normal Time (weeks)	Normal Cost	Crash Time (weeks)	Crash Cost
A	6	$6000	4	$8000
B	5	$4000	3	$5600
C	4	$6000	4	$6000
D	5	$7500	3	$8900
E	4	$2000	1	$6500
F	3	$5900	3	$5900

The following diagram shows the project time activities crashed to their lowest possible times:

A(4), C(4), E(1), F(3) 12

A(4), B(3), F(3) 10

A(4), C(4), D(3) 11

5. Can any money be saved on this project without sacrificing the minimum project completion time? If so, show the maximum amount of possible savings.

You are given the following data for a project:

Activity	Expected Activity Time in Days	Variance	Critical Path
A	7	6.1	YES
B	4	2.8	YES
C	9	1.4	NO
D	4	3.2	YES
E	6	3.1	NO
F	6	2.6	NO
G	7	1.7	YES
H	6	2.2	YES

What is the probability the project will take less than 24 days?

6. Given the following information:

Task	ES	EF	LS	LF
A	0	7	0	7
B	7	11	12	16
C	7	12	7	12
D	12	18	12	18
E	11	13	16	18
F	13	16	18	21
G	18	23	18	23
H	16	18	21	23
I	23	30	23	30

what activities are on the critical path?

The following interior activities need to be completed before the new Oil Slick auto service store can be opened. The contractor is not sure when all the work will be done, but was able to come up with the following estimates (in days).

Activity	predecessor	optimistic time	most likely time	pessimistic time
A (install floor)	----	4	7	10
B (paint)	A	5	7	15
C (install signs)	B	6	9	18
D (final cleaning)	C	2	6	10

If all these remaining activities are critical, what would be the expected completion time,

in days, of the remainder of the project?

7. The following four activities were identified as being on the critical path of a large project. The project manager wishes to reduce the completion time by three weeks. Which activity should be crashed 3rd?

Activity	Normal Time (weeks)	Normal Cost	Crash Time (weeks)	Crash Cost

A	6	$2100	4	$3300
B	9	$4200	6	$5700
C	7	$1650	6	$2100
D	6	$2000	4	$4000

8. Using PERT, the expected completion time to build a house is 85 days. The variance of the project completion time is 36. What is the probability of completing the project between 79 and 103 days?

9. For the same problem as above, what is the probability the project will take more than 73 days?

Suppose you are given the following data for a project:

Activity	Expected Activity Time (in days)	Variance	Critical Path
A	9	3.2	Y
B	6	3.2	N
C	5	2.1	Y
D	2	2.2	Y
E	11	3.4	Y
F	13	1.4	N
G	4	3.1	N
H	8	5.1	Y

10. What is the probability the project will take less than 39 days?

Suppose you are given the following information for a project:

Activity	Expected Activity Time	Variance	Critical Path
A	9	1	No
B	6	12.50	Yes
C	5	3.12	Yes
D	7	0.11	No
E	3	1.0	Yes
F	4	1.1	No
G	1	6.12	Yes

11. What is the variance of the critical path?

Given the information below, answer the following three questions:

Activity	Time (days)	Predecessors
A	5	-
B	8	A
C	3	A
D	7	C
E	5	B, C
F	2	E
G	8	D,E
H	8	F, G

12. What is the minimum completion time of the project?

13. For the same problem as above, what is the earliest time activity G can start?

14. For the same problem as above, what is the latest time the project manager could start activity C in order to not delay the project completion time?

The following information applies to the next four questions. You will need to draw the network in order to determine the critical path.

A sporting goods store is planning to open an outlet in a college town. The activities consist of the hiring of the manager of the outlet and his/her employees. Also it is necessary to coordinate the renovation of a building that previously was a fast food restaurant. To schedule this project using PERT, the following time estimates (in weeks) are gathered:

Activity	Description	Opt. time	Likely time	Pess. time	Predecessors
A	Interview at college for new manager	4	10	22	None
B	Renovate building	4	7	10	None
C	Purchase new equipment for new outlet	1	4	7	B
D	Check references for new manager and make final selection	3	3	3	A
E	Place ad for new employees & interview applicants	2	4	6	D
F	Install new equipment	2	4	12	C
G	Make final selection for employees	3	3	3	E
H	Hold orientation meetings for employees	2	2	2	F,G

Top management wants the new outlet to be opened as soon as possible. Every week that the project can be shortened will save the firm $1,000 in lease costs. There are four potential ways to save time during the project:

I. Employ an agency to locate some good prospects for the manager’s job. This approach would save one week in Activity A and costs $800.

II. By adding a few workers, the time for Activity B could be shortened by one week, at an additional cost of $200.

III. Hire another local employment agency to provide some potential employees. This could cut one week from Activity E at a cost of $900.

IV. Bring in another trainer to help with the orientation meetings. This would cut one week from activity G at a cost of $1400.

15. In how many weeks could the project be opened (without crashing any activity)?

16. How likely is it that the project will take between 19.9 and 29.2 weeks?

17. How likely is it that the project will take less than 16.8 weeks?

18. Which of the options should be taken to reduce the project completion time?

You only want to consider those activities that are on the critical path and will save you money.

I. A is on the critical path and the net savings will be: $1,000 - $800 = +$200

II. B is not on the critical path and therefore is not considered

III. E is on the critical path, and the net savings will be: $1,000 - $900 = +$100

IV. G is on the critical path, but there will be a net outlay: $1,000 - $1,400 = -$400

Given the following project data,

Activity	Normal Time (weeks)	Normal Cost	Crash Time (weeks)	Crash Cost
A	6	$2400	4	$4200
B	6	$3200	3	$3800
C	3	$2500	3	$2500
D	4	$2000	2	$2600
E	6	$2200	3	$4600
F	6	$1700	4	$3700
G	7	$2000	5	$4000

the following diagram shows the project in rationally crashed times:

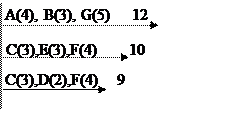
19. Can any money be saved in the diagram above without sacrificing the minimum project completion time.

Cement Construction Company has a project to undertake and they have already determined that the activities below must be performed to complete it. (times are in days)