You are a human resources researcher/analyst for a major corporation, Ourco. An executive committee wants
You are a human resources researcher/analyst for a major corporation, Ourco. An executive committee wants you to research how the company is performing on different equity and diversity dimensions.
- Your first assignment is to take a sample of executives. You propose the following types of samples to the committee. Identify what type of sample each description is (2 each for total of 8).
-
You would make a list of executives by each of five departments. You would randomly choose 4 executives out of each department
________ _________ -
A list of all the executives in the company would be compiled, and then random numbers assigned to each. Since there are about 200 executives in the company, you propose to take the 20 executives with the highest random numbers.
______ _____________ -
You would make a list of executives by each of five departments. You would randomly choose 2 departments and select all the executives in those two departments.
_______________ - You would make a list of all the executives in alphabetical order by last name, and since you want a sample of 20, , you propose to choose a random number between one and ten and then you propose to take every 10 th executive on the list.
__________
The committee decides to follow your recommendation of a simple random sample. You obtain the following data from company files; this is a random sample of all executives at the company.
| Executive | Gender | Ethnic Origin | Years Employed | Original Salary ($1000s) | Current Salary ($1000s) |
| 1 | M | Caucasian | 27 | 30 | 150 |
| 2 | M | African American | 25 | 32 | 150 |
| 3 | M | Hispanic | 25 | 30 | 150 |
| 4 | M | Other | 23 | 32 | 125 |
| 5 | M | Caucasian | 23 | 32 | 125 |
| 6 | M | African American | 22 | 32 | 125 |
| 7 | M | Caucasian | 21 | 30 | 125 |
| 8 | M | Other | 20 | 33 | 120 |
| 9 | M | Caucasian | 20 | 32 | 120 |
| 10 | M | African American | 15 | 40 | 140 |
| 11 | M | African American | 15 | 42 | 142 |
| 12 | M | Caucasian | 12 | 45 | 145 |
| 13 | M | Hispanic | 12 | 50 | 135 |
| 14 | M | Caucasian | 12 | 50 | 125 |
| 15 | F | African American | 12 | 60 | 85 |
| 16 | F | Caucasian | 12 | 55 | 85 |
| 17 | F | Hispanic | 18 | 45 | 140 |
| 18 | F | African American | 20 | 35 | 150 |
| 19 | F | Caucasian | 24 | 32 | 145 |
| 20 | F | Other | 25 | 32 | 150 |
- (11) Describe a "typical" executive using at least 2 measures of central tendency (4 points) and at least 2 measures of dispersion (4 points). You may mix and match variables and statistics as you wish – any 2 measures of central tendency and any 2 measures of variability will do (you may take one variable and discuss 4 statistics, or four variables with 1 statistic each, or anywhere in between). Draw a histogram of years with the company – interpret! (3 points).
-
The executive committee has learned that the average salary for executives in the industry is $140,000, and the committee is concerned that Ourco may not be paying enough. Using the random sample above, test the committee's idea that the mean of executive salaries at Ourco is at least equal to that of the industry standard. (Show all work as well as appropriate distribution diagrams to receive credit. You may assume = .05 and that the population is symmetrical and mounded.)
-
(2)
\[\begin{aligned}
& {{H}_{0}}:\mu \ge \text{140} \\
& {{H}_{A}}:\mu <\text{140} \\
\end{aligned}\] - (2) What is the critical value of the test statistic? __________
- (2) State the decision rule.
- (2) Sketch the sampling distribution showing the region(s) of acceptance and rejection in the graph.
- (2) Show computation and then state the statistical decision.
- (2) What would you tell the executive committee about Ourco’s salaries?
- (2) Regardless of what you have concluded, if the value of the test statistic had been t = +2.43, what would your statistical decision have been?
- (2) How do you know in which tail to perform the test?
-
(2)
-
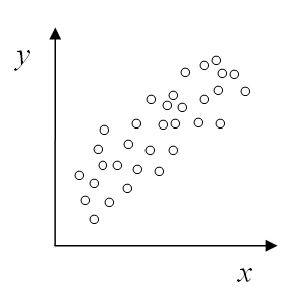
Another area of concern for the committee is that pay rates are linked, at least in large measure, to seniority (as measured by the length of time with the company). The committee realizes the relationship can’t be perfect – other factors such as merit and contribution to the company are also used to determine pay. However, the committee believes that if there is a relatively strong relationship that could be used to induce people to stay with the company. Use your calculator as needed!
-
(2) In the grid above draw the scatter for this problem. Be sure to label the axes.
- (2) Determine the correlation coefficient. How would you describe the correlation between number of years employed and current salary? (e.g. weak—moderate—strong; positive—negative) Explain your answer.
-
(3) Determine the regression equation:
- (2) Use the regression equation to predict the salary for an executive who has been with the company for 14 years. (Show your work.)
- (2) Draw the regression line on the graph.
-
(2) Why can't you predict the salary for an executive who has been with the company for 35 years?
- (2)Was the actual salary for an executive with 18 years experience more or less than expected (predicted)? Explain.
-
(2) In the grid above draw the scatter for this problem. Be sure to label the axes.
-
Using the information in #3, that the industry average is $140,000, your calculated information, and new information provided that the standard deviation of salaries in the industry is $20,000.
-
(3) Identify (- 1 for each missed up to 3):
= ______, = ______, \[\bar{x}\] = ______., s = _____, and n = _______
- (2) What is the probability that a single executive will earn $130,000 or more?
-
(2) What is the value of the standard error of the mean for this problem?
- (2) What is the probability that any sample mean of salaries of any 15 executives will be equal to or more than $130,000 per year?
-
(3) Identify (- 1 for each missed up to 3):
-
The executive committee is concerned that the sample size you used is not sufficient.
-
(5) How many randomly selected executives would you need to estimate, with a 95% confidence, the mean salary within $5,000? (Show formula & initial substitution, but use calculator!)
-
(5) How many randomly selected executives would you need to estimate, with a 95% confidence, the mean salary within $5,000? (Show formula & initial substitution, but use calculator!)
-
The committee asks you to conduct a slightly different analysis – these guys want to be thorough!
(3) Now the committee wants to know the 95% confidence interval for the mean amount paid by all other companies for executive salaries. (Show formula with values for credit.)
B (3) What would you report to the committee in terms of Ourco’s salaries based on this information?
C. (3) Explain the interval so that someone with no statistical background can understand it.
-
(8) The committee now wants to know if it could be accused of "double counting" – that is, hiring someone who meets more than one diversity criteria. The committee takes a second larger sample (salary data was not available for this sample.) and arrives at the following counts. . The committee wants to use a definition of "double counting" such that if race and gender are related (dependent), there is double-counting.
Caucasian African American All
OtherMale 72 48 28 Female 24 24 24
Test the hypothesis at the .05 level of significance that gender makes a difference in the ethnicity of the person hired.
-
(2) State the hypotheses being tested.
H o :
H a : - (2) Give the computed values of the test statistic
-
(2) State the critical value of the test statistic (
Or
give the p-value of the test.)
- (2) State and explain the decision.
-
(2) State the hypotheses being tested.
-
(11) Of course, the committee wants to know if the current average wage paid to men is different from the current average wage paid to women. The committee is sure there is not a difference.
-
(7) Test the hypothesis that there is no difference in the average wage paid based on gender. You may assume that the two populations are independent and nearly normal. You may not assume the two populations have the same standard deviations.
Show all parts of the hypothesis testing process. Points will be deducted for missing parts; however, all steps may be done using the calculator functions. (State which calculator menus were used.)
- (4) Discuss Type 1 and Type II errors in the context of this hypothesis test.
-
(7) Test the hypothesis that there is no difference in the average wage paid based on gender. You may assume that the two populations are independent and nearly normal. You may not assume the two populations have the same standard deviations.
- A. (5) The committee wants every possible angle covered. It asks you to turn this analysis around and test whether the proportion of women earning $140,000 or more is significantly different from the proportion of men earning $140,000 or more.
Show all parts of the hypothesis testing process. Points will be deducted for missing parts; however, all steps may be done using the calculator functions. (State which calculator menus were used.)
- (5) Construct a 90% confidence interval for the proportion of women (out of all of the women) earning $140,000 or more per year.
BONUS (2) Why would or wouldn’t this information be useful to the committee?
-
(9) The committee also wants to make sure that the current average wage doesn’t differ by ethnicity. Test the hypothesis that there is no difference in the average wage paid based on ethnicity. You may assume that the all populations are independent and nearly normal.
Show all parts of the hypothesis testing process. Points will be deducted for missing parts; however, all steps may be done using the calculator functions. (State which calculator menus were used.)
The following table is provided to help guide your thoughts (and analysis).Caucasian African American Hispanic Other Average Number 8 6 3 3 -
(10) QUICK ANSWERS – these do NOT depend on any thing done so far, and bear no relationship to the diversity and equality studies. 10 points total (each blank worth ½ point). Put a check mark in each box that correctly matches a particular number and whether that number COULD BE a value of the indicated statistic. For example, if 1.4 could be a probability, put a √ in the box in the first column and first row. If 1.4 could NOT be a value of an "r", leave that box (row 1, column 2) blank.
Statistic →
Value ↓p-value r r 2 t χ 2 1.4 No No No Yes Yes .5 Yes Yes Yes Yes Yes -.5 No Yes No Yes No -1.4 No No No Yes No
Instructions: Choose either 13 or 14 for bonus points! -
BONUS—Up to 4 additional points.
Discuss a specific application of statistics that either 1) has a direct effect on you or your life OR 2) is useful, or you expect to be useful, in your employment.
Deliverable: Word Document




![[Solution Library] Class Project Instructions: Analyze the data [Solution Library] Class Project Instructions: Analyze the](/images/solutions/MC-solution-library-81172.jpg)
![[See Steps] Please use the following numbers to find the following: [See Steps] Please use the following numbers](/images/solutions/MC-solution-library-81173.jpg)
![[See Solution] Homework Assignment 3 Exercise A In this exercise, [See Solution] Homework Assignment 3 Exercise A](/images/solutions/MC-solution-library-81174.jpg)