Final Exam

Mgmt 650, Fall 2009

Download the file entitled elementary.xls. This file contains data on the 100 6 ^th grade students at Oceanview Elementary School in Wichita, Kansas. Use this data to answer the questions below. Unless otherwise noted, use the 95% confidence level for all calculations.

1. Describing the Data

1. Identify each of the variables in the dataset and describe what type of variable they are (i.e. categorical, discrete numerical, ordinal, etc.). Justify your answers.
2. For the numerical data, create a table of summary statistics. Include columns for AT LEAST the mean, standard deviation, median, minimum, and maximum.

2. Sixth grade students are randomly put into classrooms every year. Three students, Michael Miller, Jose Rodriguez, and Scott Perez are best friends and want to be in the same class.

1. What is the probability that they are all in the same class?
2. What is the probability that they are all in Mr. Collins’ class?
3. What is the probability that they are all in different classes?

3. There are 100 students overall, and they are distributed into 4 classrooms of equal size. There are 54 girls and 46 boys in sixth grade at Oceanview. Calculate the probability that:

1. A class will have 15 girls
2. A class will have 15 boys
3. A class will have more than 20 girls

4. Student Height and the Normal Distribution.

1. Construct a histogram of the students height in centimeters.
2. Use the histogram and any other statistical tools that might be useful to determine if the distribution is normal.
3. Construct a histogram of the students height in inches.
4. Use the histogram and any other statistical tools that might be useful to determine if the distribution is normal.
5. The data series are obviously related…the students heights were measured in centimeters and that was converted to inches. What gives rise to any discrepancies you see, particularly in the shape of the histogram?

5. Testing for differences in student height.

1. The average height of 6 ^th grade girls in the Kansas is 61.8 inches, and the average height of 6 ^th grade boys in Kansas is 59.4 inches. Are the heights of the boys and girls at Oceanview statistically different from the statewide averages?
2. Is there a statistically significant difference between male and female height among sixth graders at this school?

6. Teacher Quality

1. Calculate and compare the means of student test scores by class.
2. Test to see if the differences in test scores are statistically significant. Which teachers have better performing students than others? Which have worse performing students?
3. Can this be used as conclusive evidence that some of the teachers are better/worse at teaching than others?
4. Repeat steps a and b using IQ scores instead of test scores. Does this change your response to part c?
5. The statewide average on the standardized test is 75. First, assume that you do not know the standard deviation for the population. How well does the school perform relative to the state average? How well does each teacher perform relative to the state average?
6. Repeat step e, this time using the fact that the statewide standard deviation of test scores is 8.
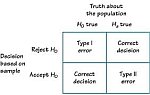
7. In parts e and f, what are the null and alternate hypotheses? Given those hypotheses, what would constitute a type I or a type II error? Did discovering the true population standard deviation in part f reveal any type I or type II errors in part e?

7. Intelligence and Test scores

1. Construct a scatter plot of IQ and test scores
2. Estimate the relationship between IQ and test scores using regression analysis
3. Interpret the Y intercept and beta coefficient. Are the results significant?
4. IQ is surely not the only determinant of student test scores. Estimate the relationship between class attendance, measured as days missing from class, and test scores.
5. Interpret the Y intercept and beta coefficient. Are the results significant?
6. Estimate test scores using BOTH IQ and attendance as independent variables. How do these relate to your answers to b-e?
7. What other variables (i.e. ones not in the dataset) do you think might be correlated with test scores? Why?

Price: $39.54

Solution: The downloadable solution consists of 21 pages, 1854 words and 5 charts.
Deliverable: Word Document