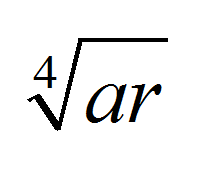Assignment 11: ANOVA (8%)

This assignment is designed as an introduction to the rationale and procedures for testing the hypothesis that the sample means for a small number of groups are equal.

Specific Steps:

1. Text: Chapter 15, One-Way Analysis of Variance. Data Analysis question 1 (a), (b), (c), (d) - pp. 329. Follow the framework of steps described in the Instructor's Comments for this week. (4 points)
2. Text: Chapter 16, Two-Way Analysis of Variance. Data Analysis question 1 (a), (b), (c) - p. 361. Follow the framework of steps described in the Instructor's Comments for this week. (4 points)

The assignment should be submitted electronically (e.g., Word file) to your instructor for marking within the time frame of the twelfth week. For every two days that an assignment is late, you will lose 1 mark unless an extension has been granted in advance. Copy appropriate tables and charts from Excel into the Word file, adding a paragraph or two to describe the nature of the data being analyzed, a couple of paragraphs describing what you did, and finally a brief description of each chart and what it shows. At the top of the Word file indicate the assignment number, the date you completed it, and your name.

The assignment should be viewed as a (very) small form of professional paper. It should follow APA style guidelines for style, spelling, and grammar. Be sure to use both the spelling check and the grammar check before submitting your assignment. Try to provide a few subheadings and be sure to number the pages.

Use the gss.sav data file to answer the following questions:

1 Question: In the General Social Survey people classified themselves as being very happy, pretty happy, or not too happy (variable happy ). Consider the relationship between happiness and age.

1 (a) Question: Compute basic descriptive statistics for each of the happiness groups.

1 (b) Question: make boxplots of age for the three groups.

1 (c) Question: Does the assumption of equal variances in the groups appear reasonable? The assumption of normality?

1 (d) Question: Perform a one-way analysis of variance on these data. What can you conclude? Which groups are significantly different from one another using the Bonferroni test?

Solution: (a) We get the following descriptive statistics:

(b) The following Box-Plots are obtained:

(c) The assumption of normality is not met, as shown in the table below:

The normality test table above shows that the groups Very Happy and Pretty Happy depart significantly from normality (p = 0.000).

The homogeneity of variances is met (p = 0.117), as shown in the table below:

(d) Using SPSS to perform an ANOVA, we get

The F-ratio is F = 6.329, and the corresponding p-value for 2 and 1384 degrees of freedom is p = 0.002. Hence, we reject the null hypothesis of equal means.

The results of the Post-Hoc test are shown below:

The mean age of the Very Happy and Not too Happy groups are not significantly different. The mean age of the Pretty Happy group is significantly lower than the mean of the other two groups.

1 Question Use the two-way analysis of variance to test the following hypotheses. Summarize your findings for each.

1 (a) Question: Average years of education (variable educ ) are the same for people employed full time and people employed part time (codes 1 and 2 for variable wrkstat ).

1 (b) Question: Average years of education are the same for males and females.

1 (c) Question: The relationship between education and work status (variable wrkstat ) is the same for males and females.

Solution: We apply a two-way ANOVA and we get the following results:

The interaction term is not significant (p = 0.117), so it makes sense to analyze the main effects separately.

• The factor Sex is not significant, which means that we fail to reject the null hypothesis that the average years of education are the same for females and males
• The factor Wrkstat is significant (p = 0.000), which means that we have enough evidence to reject the null hypothesis that the average years of education are the same for people employed full time and people employed part time

Price: $15.31

Solution: The downloadable solution consists of 8 pages, 731 words and 9 charts.
Deliverable: Word Document