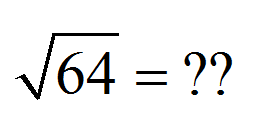1. In April 2005, a survey of students eligible to graduate in the spring was taken to determine how many expected to earn a starting salary of more than $50,000. They reported 56% of the students surveyed believed they would earn more than $50,000 in their first year out of college. (Note: a follow up study one year later indicated that only 33% of graduates had earned more than $50,000 during the year.) In 2006, the school interviewed 20 graduating students. Based on the prior year’s information:

1. What is the probability that exactly 15 of those 20 graduating in 2006 will expect earn over $50,000?
   ___________________
2. What is the probability that 11 or more of those 20 graduating in 2006 will expect to earn over $50,000?
   __________________
3. What is the probability that at least 13 of those 20 graduating in 2006 will expect to earn over $50,000
   _______________
4. What is the probability that 10 or fewer of those 20 graduating in 2006 will expect to earn over $50,000?
   __________________
5. What type of (or name of the) probability function should be used to analyze this study?
   ________________
6. What is the mean and standard deviation of this distribution? (Show your work)
   
   = _______________

=

1. Determine the following for a continuous uniform distribution between the values of 4 and 8.
   1. Draw the graph of this function.
      
      
   2. What is the probability that X is between 4.5 and 7.5?
   3. What is the probability that X is greater than 6.5?
      
   4. What is the probability that x = 7?
   5. What is the mean of this distribution?
2. The number of phone orders received per hour at an industrial supply company is normally distributed with a mean of 60 and a standard deviation of 8.

1. What is the probably that the company will receive 72 or more orders in a given hour?
2. What is the probability that the number of orders for an hour will be less than 50?
3. If the company can currently handle 64 calls in an hour what is the probability that they will get more calls than they can handle in any one specific hour?
   
4. If the company wants to have enough staff to cover incoming calls 80% of the time, how many calls do they need to be prepared to receive?

1. Determine the method of sampling that was used:
   1. The college want to determine if students would like to continue purchasing text books or would prefer to switch to a book rental system. The school randomly selects 25 course section numbers and then surveys all of the students chosen in each of those sections. What type of sampling did they use?
      ____________________
      
   2. A researcher from the CDC is gathering information from a sample of elementary schools in the Central Ohio region. She visits each school and obtains a list of the students arranged by grade level with ADD/ADHD. From these she makes a list of all of the students. She has a computer randomly generate numbers and matches these numbers to an alphabetical list of students in order to create the sample. What type of sampling did she use?
      ___________________
      
   3. For a high school project, Jenny needs to survey 20 community members about the placement of a new monument in the park in town. Jenny walks around the block near her home and samples each of her neighbors until she has 20 completed surveys. What type of sampling did she use?
      __________________
      
   4. The college want to determine if students would like to continue purchasing text books or would prefer to switch to a book rental system. The school randomly selects 20 freshmen, 40 sophomores, 60 juniors and 80 seniors to fill out the survey. What type of sampling did they use? _____________________
      
      

      ---

2. A government official is interested in determining the average monthly income of a household in their district. With some work, she is able to select a random sample of households and began to gather income information from them. The incomes – in thousands of dollars – sampled in one region were: {1.3, 3.0, 4.2, 5.8, 2.4, 4.1, 0.9, 5.7, 5.6, 2.6}. Answer the following assuming that the population is normal.
   1. What is the point estimate of the population mean? ________________
      
   2. What is the point estimate for the population variance? (Calculator function OK) ________________
      
   3. Calculate the sample standard deviation. ______________
      
   4. Explain how the sample mean is related to the population mean
   5. Assume that you know that the standard deviation of the population is 1.4 ($1,400). Construct a 80% confidence interval for \[\mu \] . (Show formula)
   6. Assume that you know that the standard deviation of the population is 1.4 ($1,400). Construct a 95% confidence interval for \[\mu \] . (Show formula) _______________
      
      
   7. Explain or interpret this interval
   8. A national survey claims that the average monthly household income in this area is $4,500. What comment can you make about this claim?
   9. Determine the needed sample size if the researcher wanted to have a 95% confidence interval with and error margin of 0.4 thousand dollars.

1. The Franklin Property and Casualty insurance company has a 80% customer satisfaction rate. The company gathers the information by surveying customers over the phone a few weeks after a claim is filed. The satisfaction of each customer is considered to be independent from the others. If 25 customers who have filed a claim in the last year are surveyed at random determine the following:

1. What type of distribution function is the model for this situation? Explain.
2. What is the expected number of satisfied customers in this group?
   ___ ___________
3. What is the variance? ________
   
4. What is the probability that exactly 20 of the 25 will respond that they are satisfied?
   _____________
5. What is the probability that at most 15 people will respond that they are satisfied?

____________

7. A quality control technician wants to determine how accurately package weights are reported on common breakfast cereals. The technician purchases 6 boxes each of Frosty Treats and Cocoa Snacks. She has the lab open the packages and weigh the contents of each. The weight is given in grams:

Frosty Treats: 362 371 368 354 376 367

Cocoa Snacks: 362 366 368 366 373 367

1. Find the average (mean), the range, and the standard deviation for each sample: (6 points)
   Frosty Treats Cocoa Snacks
   Average (Mean) ______ ______
   Range ________ ________
   Standard Deviation ____ _______
2. Based on the standard deviations calculated, which type of cereal gives the most reliable package size?? Why??

1. The following questions refer to the Sampling Distribution of the Sample Mean
   1. What makes up the data in the sampling distribution of sample mean?
      
   2. Under what two conditions will this distribution be normal?
      
      
   3. What is the mean of the Sampling Distribution of the sample mean?
      
   4. What is its standard deviation?
      
      
      
2. A population distribution is normal with a mean of 60 and a standard deviation of 20.
   1. If a piece of datum is randomly taken from this distribution what is the probability that it is less than 49?
      
      
      
      
   2. If a sample of 16 pieces of data are taken from this distribution what is the probability that the mean of the sample will be less than 49?
      
      
      
3. An instructor is trying to determine the amount of time needed to complete a particular assignment. She takes a sample of 16 students and asks each one to keep track of their time with the following results in hours:

1. Construct a 95% confidence interval for the amount of time needed for the assignment.
   \[CI=\left( 0.907376,\text{ }1.305124 \right)\]
   
2. What is the point estimate? ______
   
3. What is the margin of error of the estimate? ______
   
4. Interpret the interval

Price: $24.1

Solution: The downloadable solution consists of 8 pages, 1610 words and 1 charts.
Deliverable: Word Document