[Answer] You have been invited to present statistical information - #80201
ASSIGMENT 1:
You have been invited to present statistical information at a conference. To prepare, you must perform the following tasks:
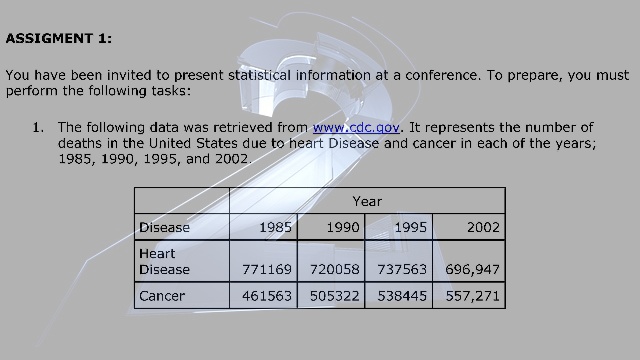
1. The following data was retrieved from www.cdc.gov. It represents the number of deaths in the United States due to heart Disease and cancer in each of the years; 1985, 1990, 1995, and 2002.
|
Year | ||||
| Disease |
1985 |
1990 |
1995 |
2002 |
| Heart Disease |
771169 |
720058 |
737563 |
696,947 |
| Cancer |
461563 |
505322 |
538445 |
557,271 |
a. Plot this data for each disease as points in a rectangular coordinate system.
b. Using a smooth line, connect your data points for each disease.
c. On a separate graph, plot only the years 1985 and 2002 and connect the points with a straight line.
d. Calculate the slope of each line.
e. Write the equation of each line in the slope-intercept form.
f. Using the equations of each line, make a reasonable prediction as to the number of deaths we might expect in 2005 due to each of these medical conditions.
2. Please include a response to this two part follow-up question with your submission.
a. Can the graphs that you constructed be classified as functions? Explain
b. Why is it reasonable that negative numbers are excluded from both the domain and rage of each of the disease graphs?
3. In the real world, what might be a situation where it is preferable for the data to form a relation but not a function?
4. There is a formula that converts temperature in degrees Celsius to temperature in degrees Fahrenheit. You are given the following data points:
| Fahrenheit |
Celsius | |
|
Freezing point of water |
32 |
0 |
|
Boiling point of water |
212 |
100 |
1. Find the linear equation that expresses temperature in degrees Fahrenheit as a function of temperature in degrees Celsius.
2. Find the linear equation that expresses temperature in degrees Celsius as a function of temperature in degrees Fahrenheit.
3. How do the graphs of these two functions differ?
ASSIGMENT 2:
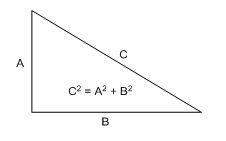
Geometry has many practical applications in everyday life. Estimating heights of objects, finding distances, and calculating areas and volumes are commonplace. One of the most fundamental theorems in geometry, the Pythagorean Theorem, allows us to make many of these calculations. The Pythagorean Theorem states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides, as shown in the diagram below.
The problems in this Unit will give you an opportunity to practice these applications.
Solve the following problems and submit them in a Word document.
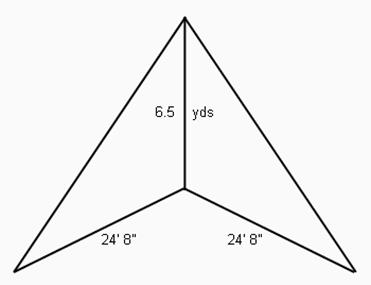
1. A Little League team is building a backstop for its practice field. It is made up of two right angles as shown below. The backstop extends 24 feet 8 inches out in each direction and the center pole is 6.5 yards high. All sides of the backstop including base and the center pole are to be made of aluminum tubing. How many feet of tubing should the team buy? How many square feet of the backstop must be covered by a screen?
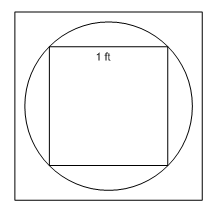
2. An Indian sand painter begins his picture with a circle of dark sand. He then inscribes a square with a side length of 1 foot inside the circle. What is the area of the circle?
3. Three buildings abut as shown in the diagram below. What are the dimensions of the courtyard and what is the perimeter of the building?

4. A cylindrical can is just big enough to hold three tennis balls. The radius of a tennis ball is 5 cm. What is the volume of air that surrounds the tennis balls?
ASSIGNMENT 3:
You are part of a panel of parents, teachers, and administrators working to revise the geometry curriculum for the local high school. On tonight's agenda, you will be brainstorming creative ways to teach surface area and volume. The teachers are especially interested in methods which will help the students connect geometry to life in the "real world" because student motivation has sometimes been lacking in this course. What suggestions do you make to the panel during your discussion? Why do you think students would benefit from this idea being used in the classroom? Explain your idea in at least two paragraphs.
Deliverable: Word Document
 and pdf
and pdf