Algebra Projects

Solution: Section Number: - #80176

GP Unit 4

Name:

Section Number:

Instructions:

Identify the document by typing your full name and section number next to the yellow text.
Rename the file by adding your last names to current file name (e.g., "u4gp_lastnames.doc").
Type your answers next to the yellow text.

Answers requiring decimal places should be rounded to two decimals. This includes rounding dollar and cent amounts to the nearest cent.

To show your work, you will need to include

o the formula with substituted values.

o the final calculated answer with units.

· To utilize the scientific calculator on your computer, do the following:

o Open the calculator (if it is not in the accessories folder, then select Run from the Start menu)

o Select View from the drop down menu

o Select Scientific to utilize the calculator.

o Note that x^y computes any number to any power (integer, fraction, decimal).

Please add your file.

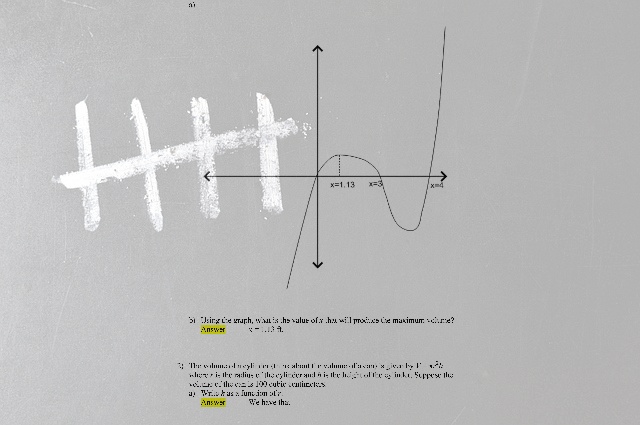
1) An open-top box is to be constructed from a 6 by 8 foot rectangular cardboard by cutting out equal squares at each corner and the folding up the flaps. Let x denote the length of each side of the square to be cut out.

a) Find the function V that represents the volume of the box in terms of x.

b) Graph this function.

c) Using the graph, what is the value of x that will produce the maximum volume?

2) The volume of a cylinder (think about the volume of a can) is given by V = πr²h where r is the radius of the cylinder and h is the height of the cylinder. Suppose the volume of the can is 100 cubic centimeters.

a) Write h as a function of r.

b) What is the measurement of the height if the radius of the cylinder is 2 centimeters?

c) Graph this function.

3) The formula for calculating the amount of money returned for an initial deposit money into a bank account or CD (Certificate of Deposit) is given by
$A=P{{\left( 1+\frac{r}{n} \right)}^{nt}}$
A is the amount of returned.
P is the principal amount initially deposited.
r is the annual interest rate (expressed as a decimal).
n is the compound period.
t is the number of years.

Suppose you deposit $10,000 for 2 years at a rate of 10%.

a) Calculate the return (A) if the bank compounds annually (n = 1).

b) Calculate the return (A) if the bank compounds quarterly (n = 4).

c) Calculate the return (A) if the bank compounds monthly (n = 12).

d) Calculate the return (A) if the bank compounds daily (n = 365).

e) What observation can you make about the increase in your return as your compounding increases more frequently?

f) If a bank compounds continuous, then the formula takes a simpler form, that is
$A=P{{e}^{rt}}$
where e is a constant and equals approximately 2.7183.
Calculate A with continuous compounding.

g) Now suppose, instead of knowing t, we know that the bank returned to us $15,000 with the bank compounding continuously. Using logarithms, find how long we left the money in the bank (find t).

h) A commonly asked question is, “How long will it take to double my money?” At 10% interest rate and continuous compounding, what is the answer?

4) For a fixed rate, a fixed principal amount, and a fixed compounding cycle, the return is an exponential function of time. Using the formula, $A=P{{\left( 1+\frac{r}{n} \right)}^{nt}}$ , let r = 10%, P = 1, and n = 1 and give the coordinates (t, A) for the points where t = 0, 1, 2, 3, 4.

a) Show coordinates in this space

5) Logarithms:

a) Using a calculator, find log 10000 where log means log to the base of 10.

b) Most calculators have 2 different logs on them: log, which is based 10, and ln, which is based e. In computer science, digital computers are based on the binary numbering system which means that there are only 2 numbers available to the computer, 0 and 1. When a computer scientist needs a logarithm, he/she needs a log to base 2 which is not on any calculator. To find the log of a number to any base, we can use a conversion formula as shown here:

${{\log }_{b}}a=\frac{\log a}{\log b}$