Problem: The following data would typically be analyzed using MANOVA.

The data below reflect information from a voluntary adoption of solar energy technology. The individuals in Group A (n = 7) have not installed a solar water heater, while individuals in Group B (n = 8) have installed the water heater. Variable W is an indicator of hot water use, and Variable G reflects automobile gasoline use.

· Use SPSS GLM and/or MANOVA to determine if differences in water and gasoline use are related to being in Group A or B.

· Suggest some directional findings in a one-paragraph summary of your findings.

· Write a brief 1-paragraph write-up of the findings....no assumption tests.

· Draw a general conclusion.

Solution: The following is obtained with SPSS:

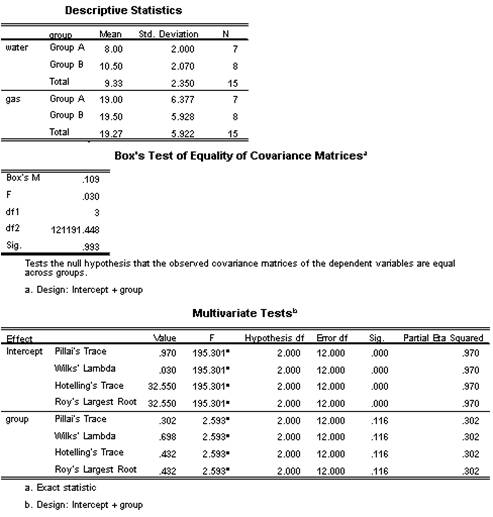
The mean for the water group A is M = 8.00 (SD = 2.00), and the mean for the gas group A is M = 19.00 (SD = 6.377). On the other hand, the mean for the water group B is M = 19.50 (SD = 2.07), and the mean for the gas group B is M = 19.00 (SD = 5.928).

The homogeneity of covariance matrices is met, F(3, 121101.4) = 0.030, p = .993 > 0.05

Based on the multivariate table, it is found that there is not a significant difference in water and gasoline use are related to being in Group A or B, F(2,12) = 2.593, p = .116 > 0.05.

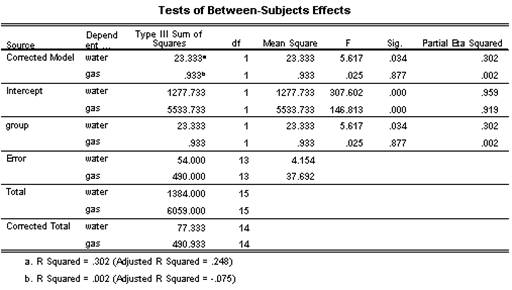
When considering the predictors individually, the assumption of homogeneity of variances is met (p = .756 and p = .864 for water and gas respectively), and iti s found that there is a significant difference in water use by groups (p = 0.034), but the difference is not significant for gas use by group (p = 0.877).