Logistic Regression Tutorial
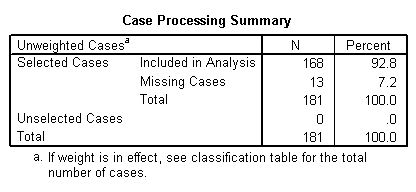
Problem: The following output has been provided which summarizes the results of a logistic regression undertaken on paired samples of failed and non-failed UK publicly quoted companies. The independent variables employed are as follows:
PBTCL_1 is profit before tax divided by current liabilities.
CLTA_1 is current liabilities to total assets.
NCI_1 is the no-credit interval which is a measure of how long (in days) a company can continue trading with no revenue being generated.
CATL_1 is current assets to total liabilities.
All of these are calculated using data taken from the last accounts published prior to failure.
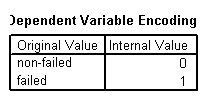
The dependent variable is dichotomous with failed companies being assigned 1 and non-failed companies 0.
Block 0: Beginning Block
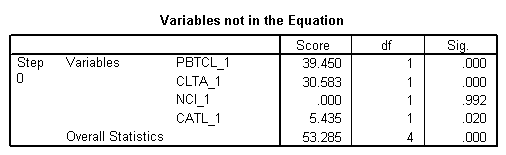
Block 1: Method = Enter
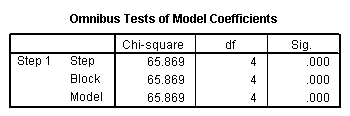

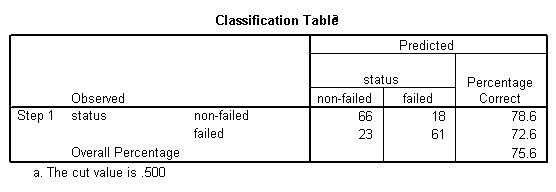
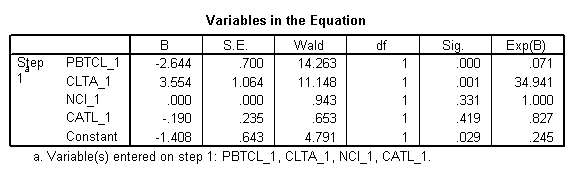
You are required to undertake a financial and statistical evaluation of this information.
Solution: Observe that the logistic model is significant overall, p = .000. Also, it is found that Nagelkerke R Square = .432, which indicates a relatively acceptable goodness of fit for this model.
It is observed that among the non-failed firms, 78.6% of them were correctly classified, whereas among the failed firms, 72.6% of them were correctly classified, which accounts for a total of 75.6% of firms correctly classified overall, which indicates a relatively good classification rate.
The logistic model is
\[\ln \left( \frac{{\hat{p}}}{1-\hat{p}} \right)=-1.408-2.644*PBTCL\_1+3.554*CLTA\_1+0.000*NCI\_1-0.190*CATL\_1\]
where \(\hat{p}\) corresponds to the probability that a firm fails. From a Financial point of view, we have the following conclusions:
· For an increase of 1 point in profit before tax divided by current liabilities, the odds of failing decrease by 92.9%. This change is significant, p = 0.000 < 0.05
· For an increase of 1 point in current liabilities to total assets, the odds of failing increase by 3294.10% This change is significant, p = 0.001 < 0.05
· For an increase of one day in no-credit interval, the odds of failing don’t change. This coefficient is not significant, p = 0.331 > 0.05
· For an increase of 1 point in current assets to total liabilities, the odds of failing decrease by 17.3% (this decrease is significant, p = 0.029 < 0.05)
