निरपेक्ष मूल्य असमानताएँ
निरपेक्ष मूल्य असमानताएँ वे असमानताएँ हैं जिनमें एक या अधिक होती हैं निरपेक्ष मूल्य . आइए याद करें कि असमानता लगभग एक समीकरण की तरह है, लेकिन "=" चिह्न के बजाय, हमारे पास "≤" या "≥" है।
यह अंतर ऐसा बनाता है कि समाधान सेट आम तौर पर एक क्षेत्र है, जैसे अधिकांश असमानताओं के लिए। और तथ्य यह है कि इसमें शामिल पूर्ण मूल्य उनके समाधान के लिए एक निश्चित विशिष्ट उपचार का संकेत देते हैं।
इस ट्यूटोरियल में हम इस प्रकार की असमानता के समाधान के लिए आवश्यक विशिष्ट कौशल पर ध्यान केंद्रित करेंगे जिसमें एक अयस्क अधिक निरपेक्ष मान शामिल हैं। साथ ही, हम यह मानेंगे कि एक या दो चर, \(x\) और/या \(y\) असमानता में शामिल हैं।
एक निरपेक्ष मूल्य असमानता क्या है?
इस विश्लेषण के प्रयोजन के लिए, हम एक निरपेक्ष मूल्य असमानता को एक या दो चरों वाली असमानता के रूप में मानेंगे, जिसमें कम से कम एक निरपेक्ष मान होगा।
उदाहरण के लिए, नीचे हमारे पास दो चर \(x\) और \(y\) के साथ एक पूर्ण मूल्य असमानता है:
\[|3x+2y-1| \ge 1\]या इसके अलावा, हमारे पास केवल एक चर के साथ निम्नलिखित पूर्ण मूल्य असमानता हो सकती है:
\[|3x-1| \le 2\]हमारे उद्देश्यों के लिए, और उनके समाधान के लिए उपयोग की जाने वाली तकनीकों के उद्देश्य के लिए, हम दोनों प्रकार की असमानताओं (एक और दो चर) से निपटेंगे।
निरपेक्ष मूल्य असमानताओं को कैसे हल करें?
समीकरणों या असमानताओं को हल करते समय, वास्तव में कोई चांदी की गोली नहीं होती है जो सब कुछ हल कर देती है। प्रत्येक समस्या अलग है और इसकी अपनी विशिष्टताएं हो सकती हैं।
हम जो सबसे अच्छा कर सकते हैं, वह यह है कि हम ऐसे कदमों की एक श्रृंखला प्रदान करें जो असमानता को हल करने की प्रक्रिया में आपकी सहायता करेंगे।
चरण 1:
प्रत्येक निरपेक्ष के लिए उन क्षेत्रों का निर्धारण करें जिनमें निरपेक्ष मान का तर्क नकारात्मक है और जहां यह गैर-ऋणात्मक है।
चरण 2:
यदि असमानता में केवल एक निरपेक्ष मान है, तो इसे दोनों क्षेत्रों में हल करें (जहाँ निरपेक्ष मान का तर्क ऋणात्मक है, और जहाँ यह गैर-ऋणात्मक है)।
चरण 3:
यदि असमानता में एक से अधिक निरपेक्ष मान हैं, तो आपको छोटे विभाजनों का एक सेट प्राप्त करने के लिए सभी क्षेत्रों को प्रतिच्छेद करना होगा। प्रत्येक विभाजन में, आपको प्रत्येक तर्क का ठीक-ठीक संकेत जानना होगा। फिर, सभी क्षेत्रों में असमानता को हल करें।
चरण 4:
एक बार जब आप भाग समाधान प्राप्त कर लेते हैं जो प्रत्येक क्षेत्र में होता है, तो अंतिम समाधान केवल इन भाग समाधानों का मिलन होता है।
सरल शब्दों में: आपको उन क्षेत्रों का पता लगाने की जरूरत है जहां आप निरपेक्ष मूल्यों के तर्क के संकेत को ठीक से जानते हैं (ताकि आप उनसे छुटकारा पा सकें)।
कुछ उदाहरणों से इन चरणों को स्पष्ट करना चाहिए।
उदाहरण 1
निम्नलिखित असमानता को हल करें
\[| 2x + 4y - 1 | \ge 2\]उत्तर:
असमानता को हल करने के लिए, हमें ऊपर बताए गए चरणों का उपयोग करने की आवश्यकता है।
चरण 1: केवल एक निरपेक्ष मान है, इसलिए हमें यह निर्धारित करने की आवश्यकता है कि तर्क नकारात्मक और गैर-ऋणात्मक है या नहीं। इसलिए, हमें पहले हल करने की आवश्यकता है:
\[2x + 4y - 1 \ge 0\]उपरोक्त को हल करने के लिए कई रणनीतियाँ हैं, लेकिन सबसे आसान है पहले समीकरण को हल करना
\[2x + 4y - 1 = 0\]जिसका अर्थ है कि \(4y = -2x + 1\) या \(y = -\frac{1}{2}x + \frac{1}{4}\) के समान, जो ढलान वाली रेखा से मेल खाती है \(m = -\frac{1}{2}\) और y-अवरोध \(n = \frac{1}{4}\)।
अब, \(2x + 4y - 1 \ge 0\) का ध्यान रखने के लिए हम परीक्षण करते हैं कि बिंदु \((0,0)\) असमानता को संतुष्ट करता है या नहीं:
\[2(0) + 4(0) - 1 = -1 < 0\]तो, \((0,0)\) असमानता को संतुष्ट करता है या नहीं। निष्कर्ष यह है कि ढलान वाली रेखा \(m = -\frac{1}{2}\) और y-प्रतिच्छेद \(n = \frac{1}{4}\) विमान को दो क्षेत्रों में विभाजित करती है:
रेखा के नीचे के बिंदुओं के लिए (हम इस क्षेत्र को 1 कहते हैं, \(R_1\)), हम पाते हैं कि \(2x + 4y - 1 < 0\)
रेखा के ऊपर के बिंदुओं के लिए, जिसमें रेखा भी शामिल है (हम इस क्षेत्र को 2 कहते हैं, \(R_2\)) हम पाते हैं कि \(2x + 4y - 1 \ge 0\)
यह महत्वपूर्ण क्यों है? हम यह सब परेशानी क्यों उठाते हैं? क्योंकि \(R_1\) पर, हम \( 2x + 4y - 1 < 0\) के बाद से \(| 2x + 4y - 1 | = -(2x + 4y - 1) \) प्राप्त करते हैं। इसी तरह, \(R_2\) पर, हमें \( 2x + 4y - 1 \ge 0\) के बाद से \(| 2x + 4y - 1 | = 2x + 4y - 1 \) मिलता है।
चरण 2: अब हमें क्षेत्र 1 पर असमानता को हल करने की आवश्यकता है, \(R_1\) :
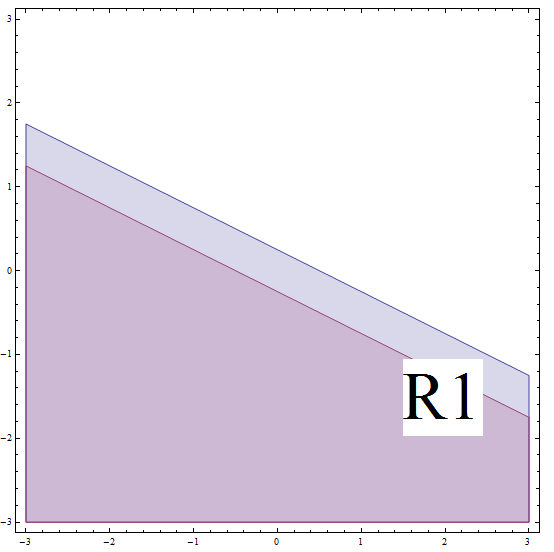
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow -(2x + 4y - 1) \ge 2\] \[\Rightarrow 2x + 4y - 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x - 1\] \[\Rightarrow y \le -\frac{1}{2}x - \frac{1}{4} \]यह ढलान \(m = -\frac{1}{2}\) और y-अवरोध \(n = -\frac{1}{4}\) के साथ नीचे या रेखा पर सभी बिंदुओं से मेल खाती है। लेकिन यह न भूलें कि आप \(R_1\) पर हैं, और यह रेखा हमने \(R_1\) की सीमा के नीचे पाई है (नीचे ग्राफ देखें)।
स्पष्ट करने के लिए, चूंकि हम इस धारणा के तहत हैं कि हम \(R_1\) में हैं, हमें यह चाहिए कि हम ढलान \(m = -\frac{1}{2}\) और y-अवरोध \(n = \frac{1}{4}\) के साथ नीचे की रेखा पर हैं। इस धारणा के तहत, हमने मूल असमानता को हल किया है और हमें ढलान \(m = -\frac{1}{2}\) और y-अवरोध \(n = -\frac{1}{4}\) के साथ लाइन से नीचे रहने की भी आवश्यकता है। ये दो स्थितियां एक साथ होनी चाहिए, इसलिए हमें दो क्षेत्रों का प्रतिच्छेदन मिलता है।
तो फिर, इस मामले में भाग समाधान नीचे के सभी बिंदुओं या ढलान वाली रेखा पर \(m = -\frac{1}{2}\) और y-अवरोध \(n = -\frac{1}{4}\) से मेल खाता है।
अब हमें क्षेत्र 2, \(R_2\) पर असमानता को हल करने की आवश्यकता है :
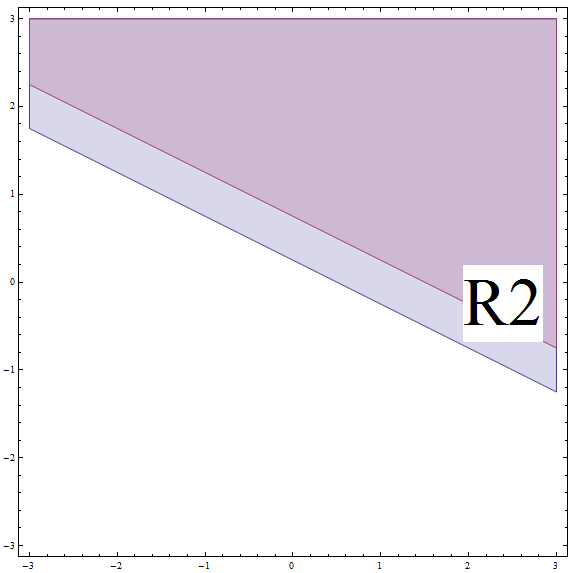
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow 2x + 4y - 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]यह ढलान \(m = -\frac{1}{2}\) और y-अवरोध \(n = \frac{3}{4}\) के साथ ऊपर या रेखा पर सभी बिंदुओं से मेल खाती है। लेकिन यह न भूलें कि आप \(R_2\) पर हैं, और यह रेखा\(R_2\) की सीमा से ऊपर है (नीचे ग्राफ देखें)।
\(R_2\) और ऊपर के क्षेत्र के बीच प्रतिच्छेदन का पता लगाने पर, हम पाते हैं कि इस मामले में भाग समाधान ऊपर के सभी बिंदु या ढलान वाली रेखा पर \(m = -\frac{1}{2}\) और y-अवरोध \(n = \frac{3}{4}\) है।
चरण 4: अब, अंतिम समाधान पिछले भागों से सभी भाग समाधानों का संघ है: अंतिम समाधान सभी बिंदु नीचे या ढलान वाली रेखा पर हैं \(m = -\frac{1}{2}\) और y-अवरोध \(n = -\frac{1}{4}\), प्लस सभी बिंदु ऊपर या ढलान वाली रेखा पर \(m = -\frac{1}{2}\) और वाई-अवरोधन \(n = \frac{3}{4}\)।
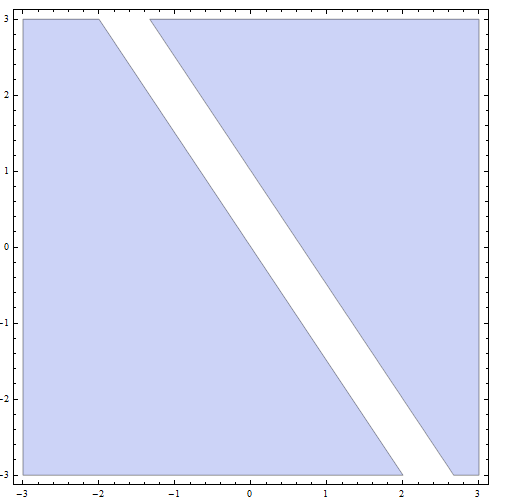
आलेखीय रूप से, हम प्राप्त करते हैं
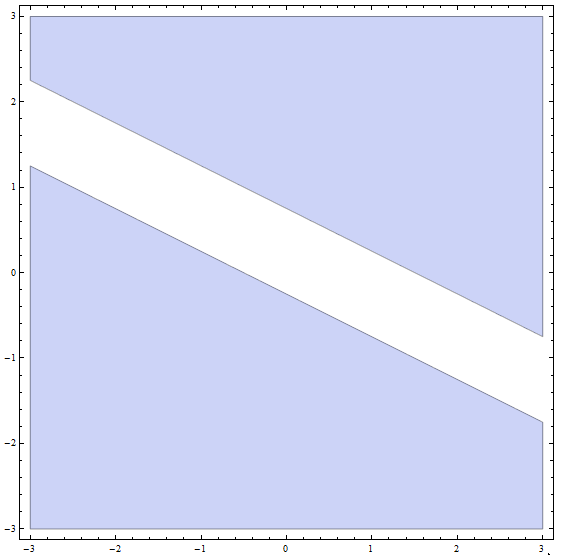
जो असमानता के समाधान को समाप्त करता है।
उदाहरण 2
निम्नलिखित डबल निरपेक्ष मान असमानता को हल करें
\[| 2x - 1 | \ge |x + 3|\]उत्तर:
यह दोहरी निरपेक्ष मान असमानता है क्योंकि 2 निरपेक्ष मान हैं। इसका मतलब है कि क्षेत्रों को खोजने में थोड़ा अधिक काम लगेगा (अपेक्षाकृत बोलना)।
चरण 1: पहले निरपेक्ष मान के लिए हम हल करते हैं:
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]तो हमें वह \(2x- 1 \ge 0\) \([\frac{1}{2}, +\infty)\) पर, और \(2x- 1 < 0\) \((-\infty, \frac{1}{2})\) पर मिलता है।
दूसरे निरपेक्ष मान के लिए हम हल करते हैं:
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]तो हमें वह \(x+3 \ge 0\) \([-3, +\infty)\) पर, और \(x+3 < 0\) \((-\infty, -3)\) पर मिलता है।
तो फिर, हम 4 क्षेत्रों को परिभाषित करते हैं:
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\)। इस क्षेत्र पर हमें मिलता है: \(2x- 1 \ge 0\) और \(x+3 \ge 0\)।
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\)। इस क्षेत्र पर हमें मिलता है: \(2x- 1 \ge 0\) और \(x+3 < 0\), हालांकि यह क्षेत्र खाली है।
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\)। इस क्षेत्र पर हमें मिलता है: \(2x- 1 < 0\) और \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\)। इस क्षेत्र पर हमें मिलता है: \(2x- 1 < 0\) और \(x+3 < 0\)।
चरण 2: अब हमें चार क्षेत्रों में से प्रत्येक पर दोहरे निरपेक्ष मूल्य असमानता को हल करने की आवश्यकता है:
• \(R_1\) को:
यहां हमें \(2x- 1 \ge 0\) और \(x+3 \ge 0\) मिलते हैं तो
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x - 1 \ge x + 3\] \[\Rightarrow \,\, 2x - x \ge 3 - (-1)\] \[\Rightarrow \,\, x \ge 4\]इसलिए, भाग समाधान प्राप्त करने के लिए हमें \(x \ge 4\), या \([4, +\infty)\) को \(R_1\) के साथ प्रतिच्छेद करने की आवश्यकता है।
इसलिए संबंधित भाग समाधान है: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• \(R_2\) को:
यह भाग समाधान खाली है (\(\varnothing\))।
• \(R_3\) को:
यहां हमें \(2x- 1 < 0\) और \(x+3 \ge 0\) मिलते हैं तो
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge x + 3\] \[\Rightarrow \,\, 2x - 1 \le -x - 3\] \[\Rightarrow \,\, 2x - (-x) \le -3 - (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]इसलिए, इस भाग समाधान को प्राप्त करने के लिए हमें \( x \le -\frac{2}{3}\), या \( (-\infty, -\frac{2}{3}]\) को \(R_3\) के साथ प्रतिच्छेद करने की आवश्यकता है।
इसलिए संबंधित भाग समाधान है: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• \(R_4\) को:
यहां हमें \(2x- 1 < 0\) और \(x+3 < 0\) मिलते हैं तो
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x - 1 \le x + 3\] \[\Rightarrow \,\, 2x - x \le 3 - (-1)\] \[\Rightarrow \,\, x \le 4\]इसलिए, इस भाग समाधान को प्राप्त करने के लिए हमें \( x \le 4 \), या \((-\infty, 4]\) को \(R_4\) के साथ प्रतिच्छेद करने की आवश्यकता है।
इसलिए संबंधित भाग समाधान है: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
चरण 4:
अंत में, हम भाग समाधानों का संघ प्राप्त करते हैं, यह प्राप्त करने के लिए कि प्रारंभिक दी गई असमानता का समाधान है
किसी ने नहीं कहा कि यह छोटा होगा, है ना? कुंआ। यह वास्तव में कठिन नहीं है, आपको बस व्यवस्थित होना है और योजना पर टिके रहना है।
निरपेक्ष मूल्य के साथ असमानताओं के बारे में अधिक जानकारी
हम इस तरह की असमानताओं की चिंता क्यों करते हैं? हम परवाह करते हैं क्योंकि उनके पास व्यवहार में अनुप्रयोग हैं।
उदाहरण के लिए, ज्यामिति में, वास्तविक रेखा में दूरियों को एक निरपेक्ष मान के रूप में प्रस्तुत करने की आवश्यकता होती है, क्योंकि इसे गैर-ऋणात्मक होना चाहिए।
एक निश्चित ज्यामितीय स्थिति हो सकती है जिसमें आपको वास्तविक रेखा में सभी बिंदुओं को खोजने की आवश्यकता होती है जो बिंदु 3 से कम से कम 2 की दूरी पर हों। ऐसी स्थिति को निम्नलिखित असमानता के साथ वर्णित किया जा सकता है:
\[| x-3 |\ge 2\]आइए उपरोक्त असमानता को समझते हैं। बिंदु \(x\) वह बिंदु है जिसे हम असमानता को संतुष्ट करना चाहते हैं। \(x\) से बिंदु 3 की दूरी को \(|x - 3|\) द्वारा दर्शाया जाता है।
फिर, हम उन बिंदुओं को खोजने की कोशिश कर रहे हैं जो बिंदु 3 से कम से कम 2 की दूरी पर हैं, इसलिए दूरी \(|x - 3|\) कम से कम 2 होनी चाहिए, जो \(|x - 3| \ge 2.\) की व्याख्या करता है।
यह सिर्फ एक तरह की निरपेक्ष मूल्य असमानताओं की समस्या है जिसे आप व्यवहार में पा सकते हैं।
क्या आप बिना किसी हल के निरपेक्ष मूल्य असमानताएँ पा सकते हैं
बिलकुल। यहां आपके पास एक \(|2x| < |x|\) है। एक असमानता के लिए यह संभव है कि यह केवल अव्यवहार्य हो जैसा कि मैंने अभी आपको दिया था।
निरपेक्ष मूल्य असमानताओं का रेखांकन कैसे करें?
उन्हें रेखांकन करने की प्रक्रिया अनिवार्य रूप से उन्हें हल करने की प्रक्रिया के साथ हाथ में है: आपको उन क्षेत्रों को खोजने की जरूरत है जहां आप जानते हैं कि निरपेक्ष मूल्यों के तर्क सकारात्मक हैं या नकारात्मक, और फिर निरपेक्ष मूल्य असमानताएं सरल असमानताओं में बदल जाती हैं, जिसे सूक्ष्म रूप से चित्रित किया गया है। फिर, प्राप्त क्षेत्रों के सभी टुकड़े आसानी से जुड़ जाते हैं।