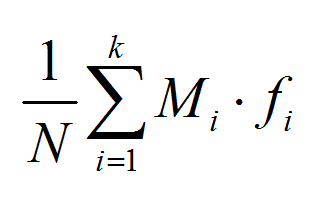इस नमूना समूहीकृत माध्य कैलकुलेटर के बारे में अधिक जानकारी

कच्चे डेटा के विपरीत, समूहीकृत डेटा होना असामान्य नहीं है। जब हम कच्चे डेटा कहते हैं, तो हमारा मतलब व्यक्तिगत डेटा होता है। तो फिर, कच्चे डेटा का मतलब है नमूने की सारी जानकारी होना।

लेकिन ऐसे मामले भी हैं जिनमें कच्चा, व्यक्तिगत डेटा ज्ञात नहीं है, और हमारे पास समूहीकृत डेटा है। इसका मतलब है, हमारे पास ऐसी जानकारी हो सकती है जैसे "नमूने में वर्ग 3 - 5 पर 4 मान हैं", जिसका अर्थ है कि हम जानते हैं कि नमूने में 3 - 5 के मानों के बीच 4 मान हैं, लेकिन हम ठीक से नहीं जानते कि वे 4 मान वास्तव में कहाँ हैं। हम केवल एक सीमा जानते हैं।

इस स्थिति में होता यह है कि हम उस वर्ग के मानों का अनुमान लगाने के लिए (हमारे सर्वोत्तम अनुमान के लिए) उस वर्ग के मध्यबिंदु का उपयोग करते हैं।

समूहीकृत डेटा के नमूना माध्य का सूत्र

समूहीकृत डेटा के लिए नमूना माध्य की गणना करने के लिए, हमें प्रत्येक वर्ग के संगत मध्यबिंदुओं की गणना करनी होगी। फिर, हमें निम्नलिखित सूत्र का उपयोग करना होगा:

\[\text{Sample Mean of Grouped Data} = \frac{1}{N}\sum\limits_{i=1}^{k}{{{M}_{i}}\cdot {{f}_{i}}}\]

जहाँ \(M_i\) i-वें वर्ग के मध्यबिंदु के अनुरूप है, और \(f_i\) i-वें वर्ग की आवृत्ति के अनुरूप है।

अन्य वर्णनात्मक सांख्यिकी कैलकुलेटर

यदि आप केंद्रीय प्रवृत्ति के माप की तलाश नहीं कर रहे हैं और इसके बजाय आप समूहीकृत डेटा के लिए फैलाव का माप चाहते हैं, तो आप इसका उपयोग कर सकते हैं समूहीकृत डेटा के लिए नमूना विचरण कैलकुलेटर .

समूहीकृत डेटा के वर्णनात्मक सांख्यिकी के अधिक पूर्ण विश्लेषण के लिए यह कैलकुलेटर . इसके अलावा, आप इसका उपयोग करने में रुचि रख सकते हैं समूहित आंकड़े के लिए प्रतिशत कैलकुलेटर , जो प्रक्षेप सूत्र का उपयोग करता है।