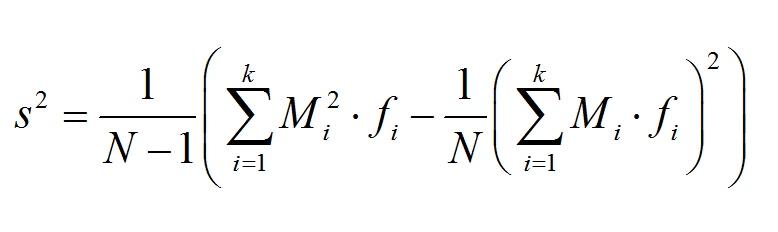समूहीकृत डेटा कैलकुलेटर के इस नमूना विचरण के बारे में अधिक जानकारी

समूहीकृत डेटा होना एक सामान्य स्थिति है, जिसमें नमूने के बारे में सभी जानकारी ज्ञात नहीं होती है। इसका मतलब है कि हम वास्तव में सभी स्कोर एक-एक करके नहीं जानते हैं। हम केवल यह जानते हैं कि एक निश्चित सीमा (एक वर्ग) के भीतर, कुछ निश्चित संख्या में मान हैं।

उदाहरण के लिए, हम जान सकते हैं कि नमूने में 4.5 और 6.5 के बीच 5 मान हैं, हालाँकि हम यह नहीं जानते कि 4.5 और 6.5 के बीच वे मान कहाँ हैं। उस उदाहरण के संदर्भ में, वर्ग 4.5 - 6.5 है, और संबंधित आवृत्ति 5 है।

समूहीकृत डेटा से निपटने का एक तरीका है। इस तरीके में क्लास के मध्यबिंदु को क्लास में उन मानों के प्रतिनिधि के रूप में समझना शामिल है। चूँकि हमें ठीक से पता नहीं है कि क्लास में वे मान कहाँ हैं, इसलिए हम उन्हें मध्यबिंदु द्वारा दर्शाना चुनते हैं। गणितीय रूप से, i-वें क्लास के मध्यबिंदु को \(M_i\) कहा जाता है।

समूहीकृत डेटा के नमूना विचरण का सूत्र

मध्यबिंदुओं को वर्गों में मानों का प्रतिनिधि मानकर, हम समूहीकृत डेटा का प्रसरण प्राप्त करने के लिए इस परिचित सूत्र का उपयोग कर सकते हैं:

\[ s^2 = \frac{ 1}{N-1}\left(\sum_{i=1}^n M_i^2 \cdot f_i - \frac{1}{N}\left(\sum_{i=1}^n M_i \cdot f_i \right)^2 \right) \]

जहाँ मान \(M_i\) मध्यबिंदु हैं, \(n\) कक्षाओं की कुल संख्या है, और \(N\) कुल नमूना आकार है।

आप इन वर्णनात्मक सांख्यिकी कैलकुलेटर को भी देखना चाह सकते हैं

आप इसका उपयोग भी कर सकते हैं समूहीकृत डेटा कैलकुलेटर का नमूना माध्य यदि आप नमूना माध्य की गणना करने में रुचि रखते हैं, क्योंकि आप फैलाव के उपायों के विपरीत केंद्रीय प्रवृत्ति के उपायों का विश्लेषण करने में रुचि रख सकते हैं

यदि आप अधिक वर्णनात्मक सांख्यिकी के कैलकुलेटर में गहराई से जाना चाहते हैं, तो इसे देखें यह कैलकुलेटर उपयोग करने के लिए एक संबंधित कैलकुलेटर है समूहित आंकड़े के लिए प्रतिशत कैलकुलेटर इसका उद्देश्य इंटरपोलेशन विधि का उपयोग करके प्रतिशतकों की चरण-दर-चरण गणना प्रदान करना है, जो उदाहरण के लिए एक्सेल द्वारा प्रयुक्त विधि से थोड़ा भिन्न है।