Calculate Area and Perimeter of a Circle
Instructions: Enter the radius \(r\) of a circle and the unit (cm, mt, ft, etc) and the solver will compute the corresponding area and perimeter.
Calculator of the Area and Perimeter of a Circle
The circle is one of the most common geometric figures, that has been known to men for thousands of years. The concept of a circle has multiple importance and applications and it has been like that since the beginning.
The unit circle in Geometry and Trigonometry has been extremely useful in the derivation of most of the common theorems we all know (or we should at least).
Despite its simplicity, it became clear to the thinker of ancient cultures that there was an extra complexity to compute area and circumference of a circle, at least with respect to what is done with squares and rectangles.
How to find the area and circumference of a given circle?
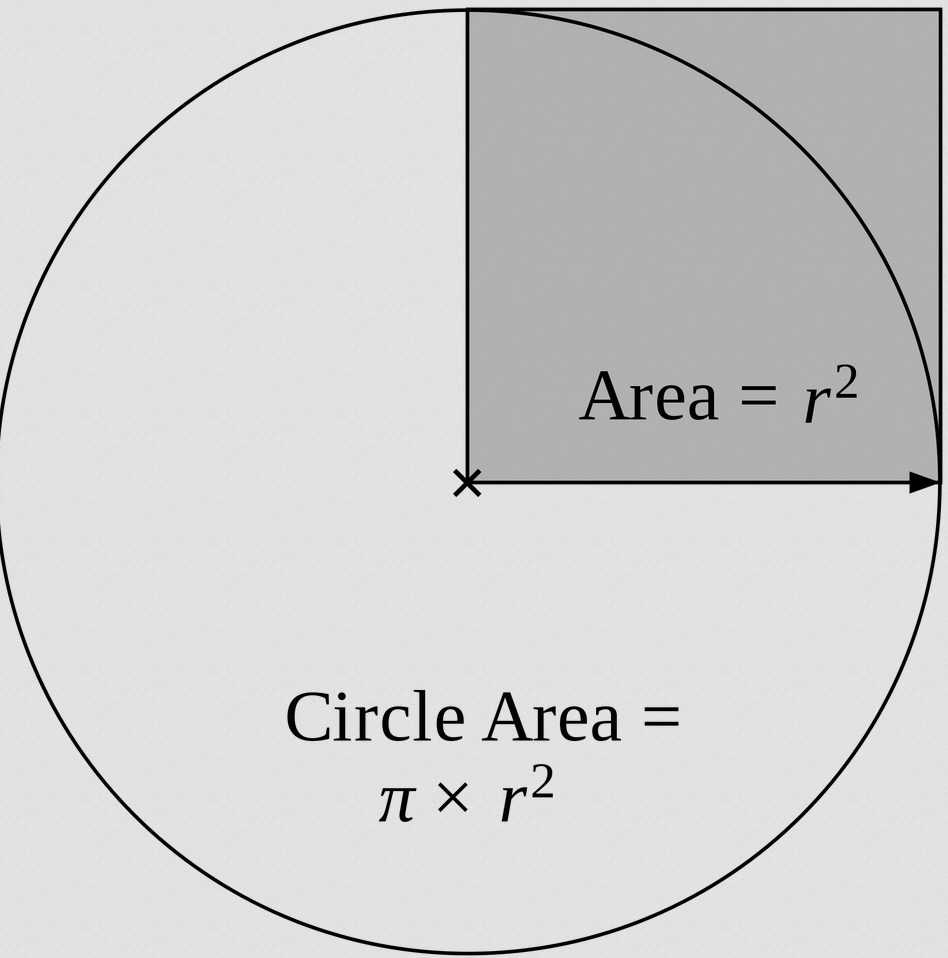
In order to compute the area and the perimeter of a circle of radius \(r\) we use the following formulas:
\[\text{Perimeter} = 2\pi r\] \[\text{Area} = \pi r^2\]Computationally speaking, it is really simple to compute the area and the perimeter of a circle, by simply plugging the radius \(r\) in the above formulas.
For example, for the case of unit circle, you have that the radius is \(r = 1\), so then the area is \(A = \pi 1^2 = \pi\).
Example of the calculation of area and circumference of a circle, for a given radius
For example, if the radius is \(r = 3\), then we compute
\[\text{Perimeter} = 2\pi r = 2\pi \cdot 3 = 6\pi\] \[\text{Area} = \pi r^2 = \pi \cdot 3^2 = 6\pi\]which completes the calculation.
deeper question would be "but, what is \(\pi\)?", and that would be an excellent question. We cannot explain in two lines what \(\pi\) is, but I can tell you at least that the mathematicians in the old times (yes, before the internet) thought that the must be a proportionality constant between the perimeter of a circle \(C\) and the diameter of a circle \(d\).
And indeed there is one for every single circle on earth, the ratio \(\frac{C}{d}\) is constant. Do you know what is that constant? Yes, you thought it right, that constant is \(\pi\).
That discovery made the old mathematicians happy, but for some reason they weren't that happy when they discovered that such proportionality constant (\(\pi\)), wasn't a rational number...
Also, this idea of the perimeter of the circle and of fractions of the circle gives rise to a more natural way of measuring angles as radians as opposed to degrees.
What if you are working with a sphere?
For the case of a sphere, you need to use this sphere area and volume calculator .