Chi-Square test for One Pop. Variance
Instructions: This calculator conducts a Chi-Square test for one population variance (\(\sigma^2\)). Please select the null and alternative hypotheses, type the hypothesized variance, the significance level, the sample variance, and the sample size, and the results of the Chi-Square test will be presented for you:
Chi-Square test for One Population Variance
More about the Chi-Square test for one variance so you can better understand the results provided by this solver: A Chi-Square test for one population variance is a hypothesis that attempts to make a claim about the population variance (\(\sigma^2\)) based on sample information.
Main Properties of the Chi-Square Distribution
The test, as every other well formed hypothesis test, has two non-overlapping hypotheses, the null and the alternative hypothesis. The null hypothesis is a statement about the population variance which represents the assumption of no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis.
The main properties of a one sample Chi-Square test for one population variance are:
- The distribution of the test statistic is the Chi-Square distribution, with n-1 degrees of freedom
- The Chi-Square distribution is one of the most important distributions in statistics, together with the normal distribution and the F-distribution
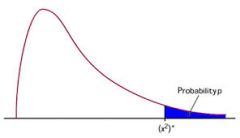
- Depending on our knowledge about the "no effect" situation, the Chi-Square test can be two-tailed, left-tailed or right-tailed
- The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true
- The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true
- In a hypothesis tests there are two types of errors. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis
Can you use Chi-square for one variable?
Absolutely! The Chi-Square statistics is a very versatile statistics, that can be used for a one-way situation (one variable) for example for testing for one variance, or for a goodness of fit test.
But it can also be used for a two-way situation (two variables) for example for a Chi-Square test of independence.
How do you do hypothesis test for single population variance?
The sample variance \(s^2\) has some very interesting distributional properties. In fact, based on how the variance is constructed, we can think of the variance as the sum of pieces that have a standard normal distribution but they are squared.
Without getting into much detail, the sum of squared standard normal distributions is tightly related to the Chi-Square distribution, as we will see in the next section.
What is the Chi-Square Formula?
The formula for a Chi-Square statistic for testing for one population variance is
\[\chi^2 = \frac{(n-1)s^2}{\sigma^2}\]The null hypothesis is rejected when the Chi-Square statistic lies on the rejection region, which is determined by the significance level (\(\alpha\)) and the type of tail (two-tailed, left-tailed or right-tailed).
To compute critical values directly, please go to our Chi-Square critical values calculator