T Distribution Graph Generator
Instructions: Make a t-distribution graph using the form below. Please type the number of degrees of freedom associated to the t-distribution, and provide details about the event you want to graph:
More About this T-distribution Graph Maker
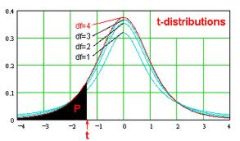
The t-distribution is a type of continuous probability distribution that takes random values on the whole real line. The main properties of the t-distribution are:
- It is continuous (and as a consequence, the probability of getting any single, specific outcome is zero)
- It is "bell shaped", in the same way the normal curves are bell-shaped
- It is determined by one parameter: the number of degrees of freedom (df). For one sample, the number of degrees of freedom is df = n - 1, where n is the sample size
- It is symmetric with respect to 0
- The t-distribution "converges" to the standard normal distribution as the number of degrees of freedom (df) converges to infinity (\(+\infty\)), in the sense that its shapes resembles more and more that of the standard normal distribution when the number of degrees of freedom becomes larger and larger.
In order to compute probabilities associated to the t-distribution we can either use specialized software such as Excel, etc, or we can use t-distribution tables (normally available at college statistics textbooks. The use of the t-distribution arises when performing hypothesis testing (for the case when the population standard deviation is not known).
In case you are rather interested in the normal distribution, you can try our normal distribution graph generator