Forty students are randomly assigned to two different groups. One group learns a list of scrambled l
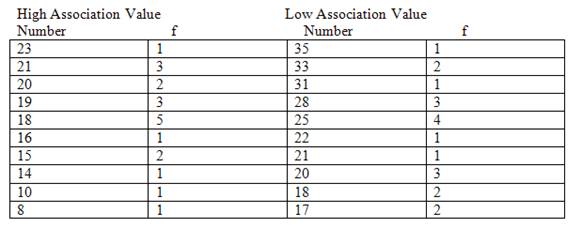
Question: Forty students are randomly assigned to two different groups. One group learns a list of scrambled letter sets with high association value (each set of letters elicits many associations), and the other group learns letter sets with low association value. The number of repetitions before an errorless recitation of the syllables is recorded for each student. The results are shown here. Compare the groups.
If you reject the null hypothesis, tell what it means in the context of the problem.
Solution: First we compute the basic descriptive statistics:
High Association Value
| Classes | M | M² | Frequency | M · f | M² · f |
| 8-8 | 8 | 64 | 1 | 8 | 64 |
| 10-10 | 10 | 100 | 1 | 10 | 100 |
| 14-14 | 14 | 196 | 1 | 14 | 196 |
| 15-15 | 15 | 225 | 2 | 30 | 450 |
| 16-16 | 16 | 256 | 1 | 16 | 256 |
| 18-18 | 18 | 324 | 5 | 90 | 1620 |
| 19-19 | 19 | 361 | 3 | 57 | 1083 |
| 20-20 | 20 | 400 | 2 | 40 | 800 |
| 21-21 | 21 | 441 | 3 | 63 | 1323 |
| 23-23 | 23 | 529 | 1 | 23 | 529 |
| Sum = | 20 | 351 | 6421 |
The sample mean is therefore
\[\bar{X}=\frac{1}{N}\sum{M_i \cdot f_i} =\frac{351}{20}={17.55}\]The sample variance is
\[s^2 =\frac{1}{N-1}\left(\sum{M_i^2 \cdot f_i-\frac{\left(\sum{M_i \cdot f_i}\right)^2}{N}}\right) = \frac{1}{20-1}\left({6421}-\frac{{351}^2}{20 -1}\right) ={13.7342}\]and the standard deviation is
\[s = \sqrt{13.7342}={3.706}\]Low Association Value
| Classes | M | M² | Frequency | M · f | M² · f |
| 17-17 | 17 | 289 | 2 | 34 | 578 |
| 18-18 | 18 | 324 | 2 | 36 | 648 |
| 20-20 | 20 | 400 | 3 | 60 | 1200 |
| 21-21 | 21 | 441 | 1 | 21 | 441 |
| 22-22 | 22 | 484 | 1 | 22 | 484 |
| 25-25 | 25 | 625 | 4 | 100 | 2500 |
| 28-28 | 28 | 784 | 3 | 84 | 2352 |
| 31-31 | 31 | 961 | 1 | 31 | 961 |
| 33-33 | 33 | 1089 | 2 | 66 | 2178 |
| 35-35 | 35 | 1225 | 1 | 35 | 1225 |
| Sum = | 20 | 489 | 12567 |
The sample mean is therefore
\[\bar{X}=\frac{1}{N}\sum{M_i \cdot f_i} =\frac{489}{20}={24.45}\]The sample variance is
\[s^2 =\frac{1}{N-1}\left(\sum{M_i^2 \cdot f_i-\frac{\left(\sum{M_i \cdot f_i}\right)^2}{N}}\right) = \frac{1}{20-1}\left({12567}-\frac{{489}^2}{20 -1}\right) ={32.1553}\]and the standard deviation is
\[s = \sqrt{32.1553}={5.6706}\]Type of Deliverable: Word Document


![[Solution] The effects of alcohol intake on aggressive driving are studied in a group of students tested on a d #25183 Hypothesis Testing - T test](/images/downloads-images/featured/Statistics-question-25182.jpg)
![[Solution] Interpret the following SPSS computer output for the chi-square test. Variable COMMUTE is “How did y #15995 Hypothesis Testing](/images/downloads-images/featured/Statistics-question-25440.jpg)

![[Solved] Replacement times for new Ford cars are normally distributed with a mean of 7.25 years and a standar #5263 Confidence Intervals](/images/downloads-images/featured/Statistics-question-8081.jpg)

