Question:

In this assignment, you examine a process that links polygons and circles. You will reach some quantitative conclusions about their respective areas and the relationship between the two.

As you know, a regular polygon has sides of equal length and angles that are the same. This confers a high degree of symmetry to these figures. A circle may be thought of as the logical limit of an n-sided polygon as n goes to infinity; the sides become infinitesimally small, and the interior angle between adjacent sides continues toward 180°.

A circumscribed polygon is a regular polygon that surrounds a circle. The radius of the circle is the length of the apothem of the polygon; both share the same center. This means the circle touches the polygon on the inside in the middle of each side of the polygon. Similarly, an inscribed polygon is surrounded by a circle sharing the same center and goes through each vertice of the polygon. A sample of inscribed and circumscribed pentagons is shown below:

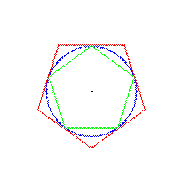
For this exercise, consider a circle of radius 1, and corresponding inscribed and circumscribed polygons with the number of sides n = 3, 4, 5, 6, and 8.

A: For each n = 3, 4, 5, 6 & 8, what are the areas of the inscribed and circumscribed polygons with n sides?