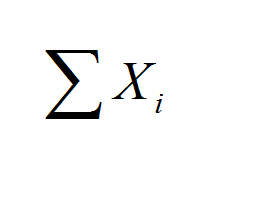Question: Find the Fourier series of the following functions on \(\left[ -\pi ,\pi \right]\) and deduce the stated formulae

1. \(f\left( x \right)=x;\,\,\,\,\,\sum\limits_{n=1}^{\infty }{\frac{1}{{{n}^{2}}}}=\frac{{{\pi }^{2}}}{6}\)
2. \(f\left( x \right)={{x}^{2}};\,\,\,\,\,\sum\limits_{n=1}^{\infty }{\frac{1}{{{n}^{4}}}}=\frac{{{\pi }^{4}}}{90}\)
3. \(f\left( x \right)={{e}^{sx}};\,\,\,\,\,\sum\limits_{n=-\infty }^{\infty }{\frac{1}{{{n}^{2}}+{{s}^{2}}}}=\frac{\pi }{s}\coth \left( \pi s \right)\)

Price: $2.99

Solution: The downloadable solution consists of 2 pages
Deliverable: Word Document