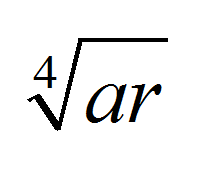Question: An automobile manufacturer plans on using 16,000 door locks in its assembly process over the next year. The firm buys these locks from a supplier who charges \(b=\\)200$ for each lot of locks delivered. Assume that the firm uses locks at a constant rate throughout the year.

1. If the cost of carrying inventories of locks is \(r=\\)10$ per unit annually, then what size lots of locks should the firm order from its supplier? How many lots should be ordered annually?
2. Suppose instead that the firm's cost per lot of locks varies directly with the size of each lot K according to \[b=2K+\frac{1}{2}\] . Given that the firm still plans on using 16,000 locks over the year and that , what lot size is optimal now? How many lots should be ordered annually? (Hint: set up the problem for minimizing total costs and solve for the new optimal lot size K* .) Intuitively, what explains the difference between your answers in parts A and B?

Price: $2.99

Solution: The downloadable solution consists of 2 pages
Deliverable: Word Document