On a study of gasoline consumption (GC), we have price of gasoline (PG) and real

income (RI) from 1975 to 1999. The regression model is:

\[G{{C}_{t}}={{\hat{\beta }}_{0}}+{{\hat{\beta }}_{1}}P{{G}_{t}}+{{\hat{\beta }}_{3}}R{{I}_{t}}+{{\varepsilon }_{t}}\]

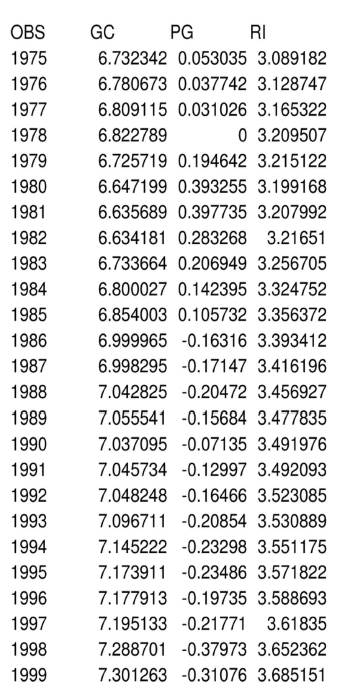
1) Estimate the model using OLS, and explain the regression output including estimated

coefficients, t test and F test. Find out which variables are significant.

2) Plot the residual by time, and explain the residual plot whether you find any problem,

any violations of seven classical assumptions of OLS? If so, what are the consequences?

3) Let's assume that we have first order serial correlation. Express the equation for the

error terms for both population and sample.

4) Carry out one side DW test. For the Durbin-Watson test, setup the hypothesis, write

the ranges of critical values at 1 percent and 5 percent significant levels (explain the

rejection, inconclusive, and accept area), and explain the whether you find serial

correlation for each confidence level.

5) Based on your conclusion, is the OLS estimator biased or unbiased, consistent or

inconsistent, efficient or inefficient?

6) Explain three cases in which the DW test is not valid.

7) What are the possible remedies if you find the serial correlation? Explain how to

estimate the GLS in this model.

8) Estimate the model using GLS and compare the results with the ones from OLS model.

Plot the residual by time, and check the serial correlation. Explain what you found.

9) Let's consider a first differenced model. Estimate the following regression model

using first differenced variables;

\[GP-G{{P}_{t-1}}={{\hat{\beta }}_{0}}+{{\hat{\beta }}_{1}}\left( P{{G}_{t}}-P{{G}_{t-1}} \right)+{{\hat{\beta }}_{2}}\left( R{{I}_{t}}-R{{I}_{t-1}} \right)+{{\varepsilon }_{t}}\]

Estimate the above model, calculate the Durbin-Watson statistic, perform the serial

correlation test at 5% significant level, and explain your finding for this model. Has the

first differencing dealt with the serial correlation problem in OLS?

Price: $58.55

Solution: The downloadable solution consists of 12 pages, and 880 words
Deliverable: Word Document and pdf