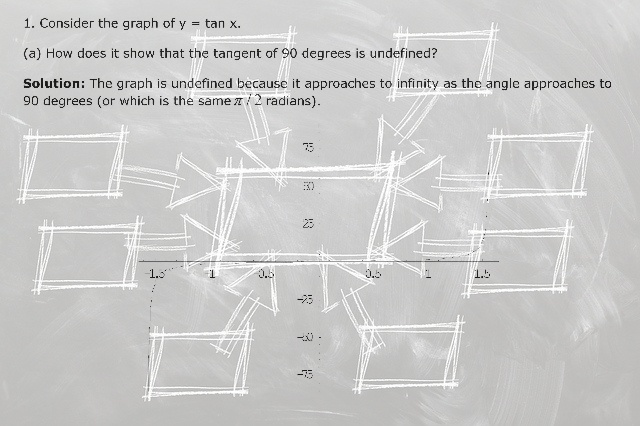
(Solved) Jason believes that sales of coffee at his shop depend - #80153
Problem 1
Jason believes that sales of coffee at his shop depend on weather. He has taken a sample of 6 days. Results are shown in columns B and C of the table. I have also performed some computations to make you task easier.
|
Column A |
Column B |
Column C |
Column D |
Column E |
Column F |
Column G |
Column H |
|
cups of |
Temp. |
B minus its mean value |
C minus its mean value |
D x E |
D^2 |
E^2 | |
|
350 |
50 |
190 |
-25 |
-4750 |
36100 |
625 | |
|
200 |
60 |
40 |
-15 |
-600 |
1600 |
225 | |
|
210 |
70 |
50 |
-5 |
-250 |
2500 |
25 | |
|
100 |
80 |
-60 |
5 |
-300 |
3600 |
25 | |
|
60 |
90 |
-100 |
15 |
-1500 |
10000 |
225 | |
|
40 |
100 |
-120 |
25 |
-3000 |
14400 |
625 | |
|
sum |
960 |
450 |
0 |
0 |
-10400 |
68200 |
1750 |
|
mean |
160 |
75 |
a. Mark the space for the dependent variable (Y): ___ cups of coffee, ___ temperature
b. Compute the equation for the least squares regression line, and report on the line provided:
______________________
Show your work in this space
c. What is the slope of the estimated regression line? _______
d. In one sentence, what does the slope indicate?
e. Compute the coefficient of determination and the correlation coefficient for temperature and the sales of coffee. Report your answers here in the spaces provided:
r2 = _________, r = _________
Show your work in this space
f. Predict sales of a 90 degree day: ______ cups (show work below).
Show your work in this space
g. Develop a 95% confidence interval for predicting average cups of coffee sold on a day when temperature is 90. Assume standard error of the estimate is 39.98.
Show work below. Report confidence interval here:
Show your work in this space
Problem 2
Age and number of hours worked per week were used to predict GPA of students. Below
you will see the Excel printout. Predict GPA of a 22-year old student who works 30 hours per week. Also, report what percentage of variability in GPA is explained by the multiple regression line.
Choose the letter corresponding to your answer from among the following and record it here: _______
A. GPA is 3.2 an variability explained is 72%
B. GPA is 3.2 and variability explained is 85%
C. GPA is 2.36 and variability explained is 48%
D. GPA is 2.36, variability explained is 43%
Problem 3
The following regression model has been proposed to predict sales at a furniture store.
\(S\) = 10 - 4X1 + 7X2 + 18X3 , where:
X1 = competitor's previous day's sales (in $1,000s)
X2 = population within 1 mile (in 1000s)
X3 = 1 if any form of advertising was used, 0 if otherwise
\(S\) = sales (in $1,000s)
a. Interpret the meaning of the coefficient of X3 in the regression model.
b. Predict sales (in dollars) for a store with competitor's previous day's sale of $3,000, a population of 10,000 within 1 mile, and six radio advertisements. Show work below, report your answer here: ____$86,000________
Problem 4
Quarterly billing for two years of water usage is shown below.
|
Year | ||
| Quarters |
1 |
2 |
|
Winter |
64 |
66 |
|
Spring |
103 |
103 |
|
Summer |
152 |
160 |
|
Fall |
73 |
72 |
|
De-seasonalized series | ||
|
Year | ||
|
Quarters |
1 |
2 |
|
Winter |
95.52239 |
98.50746 |
|
Spring |
100 |
100 |
|
Summer |
97.4359 |
102.5641 |
|
Fall |
97.33333 |
96 |
Seasonal indexes for this problem are calculated and reported in the table below.
| Winter |
Spring |
Summer |
Fall |
|
0.67 |
1.03 |
1.56 |
0.75 |
b. Use seasonal indexes to de-seasonalize the time series. Report your results in the above blank table.
c. Trend equation was calculated for the de-seasonalized data. The equation is: T = 97.3 + 0.32t. Forecast ONLY summer billing for year 3: Report answer here: _______ Show work in this space:
d. Use MAD as a measure of accuracy to determine overall effectiveness of this forecasting model. In your analysis, only include year 2. Fill out table below. Report MAD here: ____________
e. In ONE sentence, interpret the MAD value you calculated.
Problem 5
The number of cans of soft drinks sold in a machine each week is recorded below from left to right, with oldest data to the left of the table.
|
323 |
299 |
259 |
287 |
302 |
Read instructions carefully:
Develop two forecasting models which are described below, and use MAD to compare them:
· Model 1: Three period weighted moving average (weights being 5, 2, 1 respectively for one period ago, 2 periods ago and 3 periods ago).
· Model 2: Single exponential smoothing, with smoothing constant = 0.35. Use 323 as Forecast for time period 2 to start your calculations.
Fill out the table below to report your forecasts and accuracy for each model.
|
t |
Y |
Model 1 Develop Forecasts for Weighted Moving Average |
Absolute Error Model 1 |
Model 2 Develop Forecasts for Exponential Smoothing |
Absolute Error Model 2 |
|
1 |
323 |
||||
|
2 |
299 |
||||
|
3 |
259 |
||||
|
4 |
287 |
||||
|
5 |
302 |
||||
|
6 |
? |
||||
a. Based on MAD as the forecast accuracy, which of the two models should be used to forecast this time series? __ ___ Model 1 _____ Model 2
b. Use the model you selected to forecast number of cans sold in the following week: ________
Problem 6
In the space provided, draw the network for this project.
Use the 3 time estimates provided for each activity (in weeks) to estimate the expected time and variance for the activities. Then work the network forward and backward to arrive at the expected project completion time.
- What are the critical activities? _ __________________
- What is the expected time for this project? ___________ weeks
- What is the standard deviation of time for this project? _______ weeks
- What is the probability that the project will take longer than 30 weeks? __________
- What should be the promised due date if it is desired to meet that due date with a 97% probability? Answer: __________ weeks from start of the project should be set as the promised due date.
Problem 8
The life expectancy of Timely brand watches is normally distributed with a mean of four years and a standard deviation of 8 months. Please answer the following questions. Hint: Convert 4 years to months and perform/report all calculations in terms of months!
For all parts, show your work, and put your final answer on the lines provided.
a. What is the probability that a randomly selected watch will be in working condition for “more than” five years (60 months)? ___0.066807______
b. The company has a three-year warranty period on their watches (36 months). What percentage of their watches will be in operating condition “after” the warranty period? ___
c. What is the minimum and the maximum life expectancy of the “middle 95%” of the watches? Min: ______ months, Max: _______ months
d. Ninety-five percent of the watches will have a life expectancy of “at least” how many months? _________months
Problem 9
The average length of a T.V. commercial is 1.2 minutes (72 seconds). Assume the exponential distribution is applicable.
- What is the probability that a TV commercial takes less than one minute? _____________
b. What is the probability that a commercial takes between 45 seconds to 1 minute?
________________
Problem 10
A quality control manager is investigating the number of defective computer chips found in batches produced during the past week of production.
From the past week quality control records, the number of defective follows the distribution below:
|
X= no. of defectives |
f(X) |
Show your work for part c. |
|
0 |
0.15 |
0 |
|
1 |
0.2 |
0.2 |
|
2 |
0.3 |
0.6 |
|
3 |
0.2 |
0.6 |
|
4 |
0.1 |
0.4 |
|
5 |
0.05 |
0.25 |
|
Mean = 2.05 |
- What is the probability that a batch has at least 3 defective chips? __________
- What is the probability that a batch has no more than 1 defective? ___________
- On the average, how many defective units are in a batch? __________
Deliverable: Word Document
 and pdf
and pdf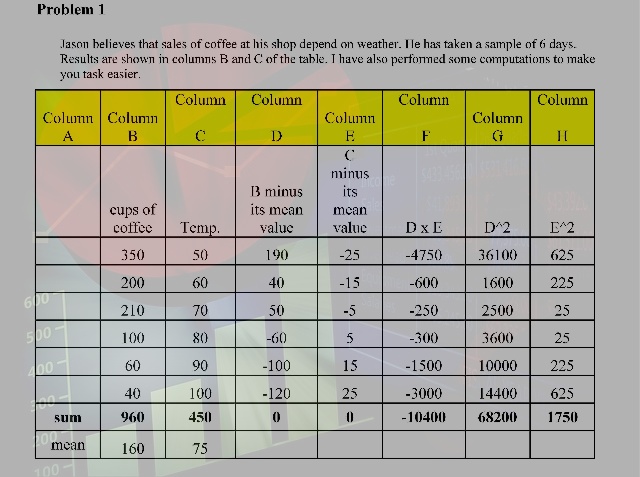



![[Solved] Work through a t-test to compare the means of two groups - #80021 Statistics](/images/projects/project-80021/statistics-1.jpg)