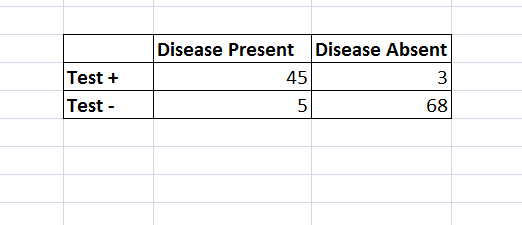
A retrospective study was done among women aged 50-54 in a rural county in Kansas who died over a six-month
- A retrospective study was done among women aged 50-54 in a rural county in Kansas who died over a six-month period. The investigators were interested in exploring the relationship between a high-salt diet (a risk factor for cardiovascular problems) and death. The investigators attempted (unsuccessfully) to include an equal number of women who died from cardiovascular diseases (CVD) (the ‘cases’) and women who died from other causes (the ‘controls’). It is found that 35 women who died from CVD, five were on a high-salt diet before they died, whereas of 25 women who died from other causes, two were on such a diet. These data are summarized below.
Cause of Death
| CVD | Non-CVD | |||||
| Diet | High-salt | 5 | 2 | 7 | ||
| Low-salt | 30 | 23 | 53 | |||
| 35 | 25 | 60 |
- Compute the table of counts that would be expected to occur in each of the four cells if the variables cause of death and diet were independent. (Copy the original table and change the entries in the table.)
- Write down the two tables that are less supportive of the null than the one observed.
- You will find the raw data for question in CVD.mtw and CVD.sav. Obtain a contingency table showing the percentage of each Cause of Death group that had a high salt diet. Summarize the results.
- Try performing a Chi-square test of Independence for these data; explain the significance of any error messages. Perform the FET and carefully state your conclusion (in context, of course).
2. In my introductory statistics class last year 14 of the class were lower-class women (Freshmen or Sophomores) and 11 were Upper-class women (Juniors or Seniors). Two of the Lower-class women but only one of the Upper-class women failed the course. Enter these data into SPSS in the form of two columns (Class and Outcome). You may regard these students as a random sample of Simmons students who take Intro. Stat.
- Perform a Chi-Square Test for Independence in this case. Paste in the output. Do you see any problem with this test? Explain.
- Perform a two-sided Fisher’s Exact Test. What are the null and alternative hypotheses? What conclusion is appropriate?
3. The table below displays the results of a study investigating the effectiveness of bicycle safety helmets in preventing head injury, The data consists of a random sample of 793 individuals who were involved in bicycle accidents during a specified one-year period.
| Wearing Helmet | |||
| Head Injury | Yes | No | |
| ---------------------------------------------------------------------------- | |||
| Yes | 17 | 218 | |
| No | 130 | 428 | |
- What are the odds of a head injury for riders not wearing a helmet? What are the odds of a head injury for riders wearing a helmet? Compute the sample odds ratio (as a number greater than one). Interpret your answer.
- Compute a 90% confidence interval for the corresponding population odds ratio.
- Use you interval in part (b) to test whether these two variables are independent. Be sure to state your hypotheses and your conclusions.
4. Open the data set Maternal.sav . I would like you to explore the relationship between the variables "whether or not low birth-weight" and parity. Recall that in this example parity is defined as 0 if the infant was the mother’s first born and 1 otherwise. Add suitable value labels for parity.
- Obtain a contingency table showing the percentage who are low birth-weight broken down by parity. Summarize the results. Does there seem to be a relationship between these two variables?
- What are the odds of a low-birth-weight among first-born infants? What are the odds of a low-birth-weight among non-first-born infants? Obtain the odds ratio (as a number less than 1).
- Compute a 95% confidence interval for the corresponding population odds ratio.
- Use you interval in part (c) to test whether these two variables are independent. Be sure to state your hypotheses and your conclusions.
- In part (c) you computed a 95% confidence interval for the population odds (of a low BWT infant) associated with being not first-born. Without going through the entire process that you went though in part (c) obtain a 95% confidence interval for the population odds (of a low BWT infant) associated with being first-born.
- Is your conclusion in part (c) consistent with your answer to part (a)? Explain.
5. Refer to the data in Q. 1 in Assignment M6. The raw data is in a file Bully. sav (in the Table of Contents for this module). Use four different techniques to test the null hypothesis that the two variables are independent against the alternative the two variables are dependent. There is no need to write separate conclusions. Write a single conclusion that contains (a) the summary of the sample data and (b) a conclusion (based upon your four tests) about the relationship between size and whether or not bullied.
6. Your room-mate (Kelly-Kate) is taking a biostatistics course at BU. She has been told to use three difference statistical tests to test for independence in a two-by-two contingency table. She shows you the following results:
Two proportion Z Test p-value = 0.248
Chi-square Test for Independence p-value = 0.250
Fisher’s Exact Test p-value = 0.324
Kelly-Kate’s instructor has asked her to come with some kind of merged p-value. What would you suggest?
Deliverable: Word Document


![[See Solution] Guide to reports INTRO (2 paragraphs)- give some background [See Solution] Guide to reports INTRO (2](/images/solutions/MC-solution-library-81936.jpg)

![[See Solution] Introduction The objective of this course is not only [See Solution] Introduction The objective of this](/images/solutions/MC-solution-library-81938.jpg)
![[Steps Shown] An analyst hypothesizes that the Peter Principle [Steps Shown] An analyst hypothesizes that the](/images/solutions/MC-solution-library-81939.jpg)
![[Step-by-Step] Fox Enterprises is considering six projects for possible [Step-by-Step] Fox Enterprises is considering six projects](/images/solutions/MC-solution-library-81940.jpg)