Indicate whether the following statements are valid: P(A and B) = .5 ______ ______ P(A or B) = -0.3 ______
- Indicate whether the following statements are valid:
- P(A and B) = .5 ______ ______
- P(A or B) = -0.3 ______ ______
-
P(A) = 0.6; P(A’) = 0.5
______
______
Recall is the correlation coefficient: - = -0.3 ______ ______
- = 1.3 ______ ______
2. The probability an employee expects to change jobs voluntarily in the next three years given they are male is 0.20. The probability an employee expects to change jobs voluntarily in the next three years given they are female is 0.40. Suppose half of those surveyed were females.
- What is the probability a person is female?
- What is the probability a person male?
- What is the probability a person is male if they expect to change jobs voluntarily in the next three years?
- What is the probability of selecting a male who does not expect to change jobs voluntarily?
- Are changing jobs and being male independent? Why or why not?
- Are changing jobs and being male mutually exclusive? Why or why not?
3. Assuming the following data comes from a random sample,
Find a 98% confidence interval for the true mean Current Salary of bank employees:
4. Short Answers
-
Complete the following probability distribution:
x 2 4 6 8 10 12 P(X=x) 0.15 0.35 0.05 0.35 0.05 0.10
Consider the following data values: 4, 6, 10, 5, 3, 10 - What is the range? _______
- What is the minimum? _________
- What is the maximum? _________
- What is the median? __________
- What is the mode? __________
- What is the mean? _________
5. Given the following table, test whether there is a positive correlation between educational level and current salary (use = 0.05)
- What is the estimated correlation coefficient? __________
- Is there a statistically significant positive correlation? Why or why not?
d. What percent of variation in Current Salary is explained by educational level? __
Coefficients(a)
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | ||
| B | Std. Error | Beta | ||||
| 1 | (Constant) | -7332.471 | 1128.765 | -6.496 | .000 | |
| EDUCATIONAL LEVEL | 1563.963 | 81.819 | .661 | 19.115 | .000 | |
a Dependent Variable: CURRENT SALARY
Using the above table,
e. Write the least squares regression equation.
f. Interpret the slope on educational level (measured in years of education)
g. What is the predicted Current Salary for an employee with 12 years of education? _________
6 . Given the following table, test whether current salary differs, on average, by gender (use = 0.01)
-
H0:
H1: - What is the test statistic value? _________
- Does current salary differ, on average, by gender? Why or why not?
7. Test whether gender and being a clerical worker are independent.
-
Clearly state the null and alternative hypotheses:
H 0 :
H 1 : - Degrees of freedom: _______
- Critical value: ______
- Conclusions:
SEX OF EMPLOYEE * CLERICAL Crosstabulation
Count
| CLERICAL | Total | |||
| clerical | nonclerical | |||
| SEX OF EMPLOYEE | MALES | 100 | 200 | 300 |
| FEMALES | 100 | 100 | 200 | |
| Total | 200 | 300 | 500 | |
Assignment 2
-
The personnel office at a large electronics firm regularly schedules job interviews and maintains records of the interviews. From the past records, they have found that the length of a first interview is normally distributed with mean =35 minutes and standard deviation =7 minutes.
- What is the probability that a first interview will last 40 minutes or longer?
- Nine first interviews are usually scheduled per day. What is the probability that the average length of time for the nine interviews will be 40 minutes or longer?
- Assume that IQ scores are normally distributed with standard deviation of 15 points and mean of 100 points. If 100 people are chosen at random, what is the probability that the sample mean of IQ scores will not differ from the population mean by more than two points?
- A random sample of 49 medical doctors in Los Angeles showed that they worked an average of 53.1 hours/week. Find a 95% confidence interval for the mean number of hours worked by all Los Angeles doctors. (assume is known and equals 7.2 hours/week)
- How large a sample is needed in Problem 3 if we want to be 99% confident that our point estimate is within 1 hour of population mean? (again assume =7.2)
-
The Summa is a new sports car. An extended transmission warranty is available for $1500 that will replace or repair the transmission if it fails during the first 65,000 miles. The normal warranty period is for 24,000 miles. A random sample of eight Summas were driven under a variety of conditions until the transmission failed. The mileage at the time of transmission failure was recorded. These data are (in miles) Assume mileages are normally distributed.
75,436 80,212 42,316 25,415
61,335 50,720 52,318 66,143
The following table provides sample information for the above data.
Find a 90% confidence interval for mileage at the time of transmission. - According to the Energy Information Association (as reported in USA Today March 15, 1994) the average annual miles driven per vehicle in the United State is 10.6 thousand miles. Suppose that a random sample of 36 vehicles owned by residents of Chicago showed that the average mileage driven last year was 10.2 thousand miles with standard deviation 600 miles. Does this indicate that the average miles driven per vehicle in Chicago is different (higher or lower) than the national average? Use a 0.05 level of significance.
- Two competing companies make TV picture tubes. A random sample of 100 Nippon tubes showed that the mean lifetime was 6.3 years with standard deviation 0.8 years. Another random sample of 100 Sunnyvale tubes showed that the mean lifetime was 6.2 years with standard deviation 0.5 years. Do the data indicate that the Nippon tubes last longer? (Use a 1% level of significance.) (Assume population variances known 1 =0.8 2 =0.5)
- The Quickie Cake Mix Company has decided to market gingerbread mixes. They have two recipes they could market. Recipe A is easier to make than recipe B, so they prefer to use recipe A unless a higher proportion of people favor recipe B. Of a random sample of 62 people were given a taste from recipe B, and 41 said they liked it well enough to buy the mix. Use 1% level of significance to test the claim that a higher proportion of people might purchase the recipe B mix.
-
An independent rating service is trying to determine which of two hamburger stands has quicker service. Over a period of 16 randomly selected times the average waiting period at Burger Queen is 4.8 min with standard deviation 2.0 min. The average waiting period at McGregor over a period of 14 randomly selected times is 5.2 min with standard deviation 1.8 min. Using a 5% level of significance, can we say there is a difference in the average waiting time at Burger Queen and McGregor? (Assume variances unknown, but equal and waiting times are normal)
. - Please use Excel :
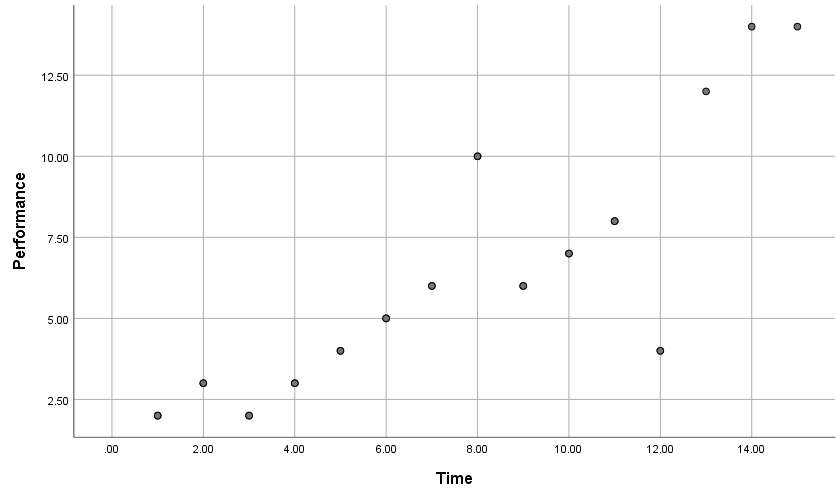
A sociologist is interested in the relation between x=number of job changes and y=annual salary (in thousands of dollars) for people living in the Nashville Area. A random sample 10 people employed in Nashville provided the following information:
x ( No. of job changes) | 4 7 5 6 1 5 9 10 10 3
y (Salary in $1000) | 33 37 34 32 32 38 43 37 40 33
- Draw a scatter diagram for the data
- Looking at the scatter diagram and least-squares line, do you think the correlation coefficient will be positive, negative, or zero?
- Looking at the scatter diagram and least-squares line, do you think the slope will be positive, negative, or zero?
- Find r. Find the coefficient of determination.
- Test the claim that the population correlation coefficient is positive (use a 5% level of significance).
- Find the sample means for Number of job changes and Salary (in $1000).
- Estimate the equation of the least-squares line.
- Graph the least-square line on your scatter diagram.
- What is the estimated salary for someone with 2 job changes?
- Find a 90% confidence interval for the coefficient on number of job changes.
- Test the claim that the slope coefficient is positive (use a 5% level of significance).
Recall r is the correlation coefficient.
- a) Fill in the blank: x-bar is to as r is to ______.
b) The coefficient of determination is the _____________ of the correlation coefficient.
12. Identify the relationship between two variables and the terminology used to describe that relationship if:
(a). r > 0 (b) r=0 (c) p< 0
13. Reading Nook Bookstore has 750 retail outlets across the country. The sales director wanted to see if Christmas music affects book sales in December. She randomly assigned some of the outlets to pipe in music and others not to. Then sales records for the month of December were kept. The results are shown in Table 11-11. Test the hypothesis that sales and Christmas music are independent. Use a 0.05 level of significance.
| Outlet | Less than 10,000 | 10,000-20,000 | More than 20,000 | Row Total |
| With Music | 5 | 18 | 7 | 30 |
| Without Music | 10 | 7 | 3 | 20 |
| Column Total | 15 | 25 | 10 | 50 |
2 test = 6.361
Deliverable: Word Document



![[Step-by-Step] PETFOOD The marketing manager of a large supermarket [Step-by-Step] PETFOOD The marketing manager of a](/images/solutions/MC-solution-library-80792.jpg)