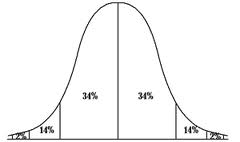
1. a)
   

Given the above graph, identify the graph of the function (line, parabola, hyperbola, or exponential), explain your choice, and give the domain and range as shown in the graph, and also the domain and range of the entire function.

Graph Type

Explanation

Domain
Range

b)

Given the table above, graph the function, identify the graph of the function (line, parabola, hyperbola, or exponential), explain your choice, and give the domain and range as shown in the graph, and also the domain and range of the entire function.

Graph

Graph Type

Explanation

Domain

Range

c)

Given the graph above, identify the graph of the function (line, parabola, hyperbola, or exponential), explain your choice, and give the domain and range as shown in the graph, and also the domain and range of the entire function.

Graph Type
Explanation
Domain
Range

d) In most businesses, increasing prices of their product can have a negative effect on the number of customers of the business. A bus company in a small town has an average number of riders of 1,000 per day. The bus company charges $2.00 for a ride. They conducted a survey of their customers and found that they will lose approximately 50 customers per day for each $.25 increase in fare.

Given the description above, graph the function, identify the graph of the function (line, parabola, hyperbola, or exponential), explain your choice, and give the domain and range as shown in the graph you have drawn, and also the domain and range of the entire function excluding unrealistic values.  The vertical axis is the number of riders per day, and the horizontal axis is the fare.

Graph

Graph Type

Explanation

Domain

Range

2) For the function,

1. Give the y values for x = -2, -1, 0, 1, 2, 3

Answer:

Show work in this space.

• \(\frac{1}{-2-1}=\)
• \(\frac{1}{-1-1}\)
• \(\frac{1}{0-1}\)
• \(\frac{1}{1-1}\)
• \(\frac{1}{2-1}\)
• \(\frac{1}{3-1}\)
  

b) Using these points, draw a curve.
Show graph here.

3) It is approximately 300 miles from Chicago, Illinois, to St. Louis, Missouri. Allowing for various traffic conditions, a driver can average approximately 60 miles per hour.

a) Write a linear function that expresses the distance traveled, d , as a function of time, t .

Answer:


b) How far have you traveled after 3 hours?

Obtain the solution from the equation in 3a), do not just guess.

Answer:

Show work in this space.

c) Write a linear function that expresses the distance to be traveled to reach St. Louis, s , as a function of time, t .

Answer:

Show work in this space.

d) How far will I need to travel to reach St. Louis after I have traveled 3 hours?

Answer:

Show work in this space

Price: $13.35

Solution: The downloadable solution consists of 7 pages, 635 words and 6 charts.
Deliverable: Word Document