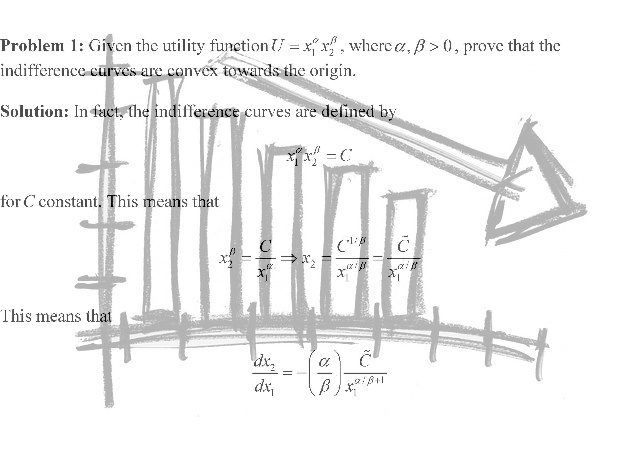
Problem 1: Given the utility function \(U=x_{1}^{\alpha }x_{2}^{\beta }\), where \(\alpha ,\beta >0\), prove that the indifference curves are convex towards the origin.

Problem 2: Prove that a diminishing marginal rate of substitution neither implies nor is implied by diminishing marginal utility.

Problem 3:

(i) maximizing \(U={{({{x}_{1}}{{x}_{2}})}^{3}}+{{x}_{1}}{{x}_{2}}\), subject to \({{p}_{1}}{{x}_{1}}+{{p}_{2}}{{x}_{2}}=y\), and

(ii) maximizing \(U=\ln {{x}_{1}}+\ln {{x}_{2}}\), subject to \({{p}_{1}}{{x}_{1}}+{{p}_{2}}{{x}_{2}}=y\)

and explain the relation between the solutions.

Price: $24.95

Solution: The downloadable solution consists of 6 pages, and 277 words
Deliverable: Word Document and pdf