1. Determine the indefinite integral
   \(I=\int\left(x^{4}+1\right)^{2} d x\)
2. Find
   \(\int \frac{1}{2} d x\)
3. A certain automobile gets 28 miles per gallon of gasoline for speeds up to 50 miles per hour. Over 50 miles per hour, the number of miles per gallon drops at the rate of 12 percent for each 10 miles per hour.

1. If \(s\) is the speed and \(y\) is in miles per gallon, find \(y\) as a function of \(s\) by solving
   \(\frac{d y}{d s}=-0.012 y, \quad s \geq 50\)
2. What gasoline mileage can you expect at \(66.9 \mathrm{~m} / \mathrm{s}\) ? Answer in units of \(\mathrm{mi} / \mathrm{gal}\).

5. A particle moves in a straight line with velocity \(v(t)=3 t^{2}-6 t .\) If it initially starts moving from 0 (where \(x=0)\), then its position \(x(t)\) is equal to

6. An evergreen nursery usually sells a certain shrub after 6 years of growth and shaping. The growth rate during those 6 years is approximated by

\(\frac{d h}{d t}=0.5 t+2\) where \(t\) is the time in years and \(h\) is the height in inches. The seedlings are 5 inches tall when planted (at \(t=0\) ).

1. Find the height after \(t\) years.
2. How tall are the shrubs when they are sold? Answer in units of inches.
   8. An object falling from rest encounters air resistance that is proportional to its velocity. If the acceleration due to gravity is considered to be \(-32\) feet per second per second, the net change in velocity is
   \(\frac{d v}{d t}=k v-32 .\) a) Find the velocity of the object as a function of time if the initial velocity is \(v_{0}\).
   b) Find the limit of the velocity as \(t\) approaches infinity.
3. Find the position function \(s(t)\).

11. Evaluate

\(\sum\limits_{i=1}^{15}{\frac{1}{{{n}^{3}}}{{\left( i-1 \right)}^{2}}}\)

12. Find the following limit

\(\underset{n\to \infty }{\mathop{\lim }}\,\sum\limits_{i=1}^{\infty }{{{\left( 1+\frac{2i}{n} \right)}^{3}}\left( \frac{2}{n} \right)}\)

13. Express

\(\lim _{\|\Delta n\| \rightarrow 0} \sum_{i=1}^{n} \sqrt{c_{i}^{2}+4} \Delta x_{i}\) as a definite integral on [0,3], where \(c_{i}\) is any point in the \(i^{\text {th }}\) subinterval.

14. Evaluate

using Riemann sums.

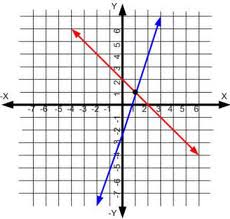
15. The graph of \(f\) is shown in the figure.

If \(\int_{1}^{3} f(x) d x=2.3\) and \(F^{\prime}(x)=f(x)\), find \(F(3)-F(0)\)

16. Find

\(\int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}}\left(1+\cot ^{2} x\right) d x\)

17. Find the area of the region bounded by

\(y=|x|, x=-2, x=2,\)

and the \(x\) -axis.

18. Evaluate

\(\int_{3.9}^{7.2}-3 x d x\)

19. Find \(F^{\prime}(x)\) for

\(F(x)=\int_{8}^{x} \sqrt[3]{t} d t\)

20. Find the value guaranteed by the Mean Value Theorem for Integrals for

\(f(x)=\frac{9}{x^{3}}\)

over [1, 3.9].

21. Determine the value(s) of \(x\) at which

\(f(x)=\int_{-2}^{x^{2}+4 x} e^{t^{2}} d t\) has a local minimum.

22. a) Find the open intervals of \(x\) on which

\(y=x e^{x}\)

is increasing

b) Find the \(x\) -values of all relative extrema.

24. Find

\(\int e^{x} \sqrt{1-e^{x}} d x\)

25. Find \(\frac{d y}{d x}\) for

26. Find \(f^{\prime}(x)\) for

\(f(x)=5^{x-2}\)

Price: $14.86

Solution: The downloadable solution consists of 10 pages, 486 words and 2 charts.
Deliverable: Word Document