More about this Normal Distribution Grapher

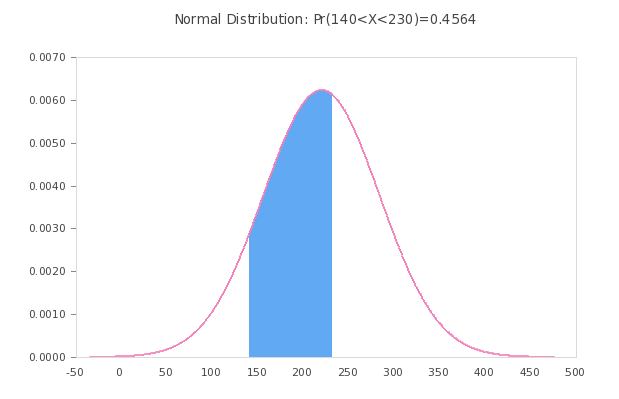
You can use this tool to graph an event in the context of a normal distribution. Your need to provide the population mean \(\mu\) and population standard deviation \(\sigma\) and this normal graph generator will highlight the region your are interested in. Also, you can compute the normal distribution probability associated to this event.

This normal probability graph generator will shade the region in the normal distribution corresponding to the event that you specified.

Normal versus T-distribution

Often times you are at a situation in which the population standard deviation is not known. For those case, you will want to use the t-distribution instead of the normal distribution, and then you will need this t-distribution graph generator instead. For the t-distribution, all you need to specify is the number of degrees of freedom.

Applications for this Normal Probability Graph maker

You can find applications to the normal distribution and its graph in virtually every scientific discipline. And this is not because all distributions are normal, because that is not the case, it is rather due to the Central Limit Theorem.

The CLT states that for ALL distributions, regardless of their shape, the sampling distribution will be approximately normal if the sample size is large enough.

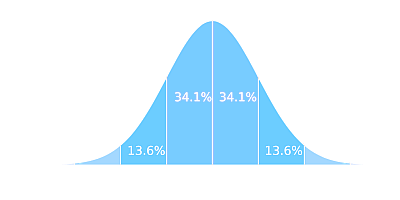
Another common use for this graph maker is to illustrate the regions described by the empirical rule, which is approximately 68% for within one standard deviation from the mean, 95% for within two standards deviation from the mean and 99.7% for within three standards deviation from the mean.

Depending on the context, you may want to find the score X such that for a given p value, the probability that scores are to the left of X is exactly equal to p. This can be achieved with this invnorm calculator online, or by using statistical software such as Excel.