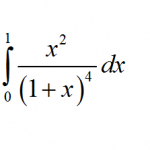Table of Integrals

1 .-) \(\displaystyle \int x^n, dx = \frac{x^{n+1}}{n+1}+C, \qquad n \ne -1\)

2 .-) \(\displaystyle \int \frac{dx}{x}=\ln |x|+C\)

3 .-) \(\displaystyle \int a^x , dx=\frac{a^x}{\ln a}+C\)

4 .-) \(\displaystyle \int \tan x, dx = \ln|\sec x|+C\)

5 .- ) \(\displaystyle \int \cot x, dx = \ln|sin x|+C\)

6 .- ) \(\displaystyle \int \sec x, dx = \ln |\sec x+\tan x|+C\)

7 .- ) \(\displaystyle \int \csc x, dx = \ln |\csc x-\cot x|+C\)

8 .- ) \(\displaystyle \int \frac{dx}{x^2-a^2}=\frac{1}{2a} \ln \left| \frac{x-a}{x+a}\right|+C, \text{ if } x^2>a^2\)

9 .- ) \(\displaystyle \int \frac{dx}{x^2-a^2}=\frac{1}{2a} \ln \left| \frac{a-x}{x+a}\right|+C, \text{ if } a^2>x^2\)

10 .- ) \(\displaystyle \int \frac{dx}{x^2+a^2}=\frac{1}{a}\arctan\left(\frac{x}{a}\right)+C\)

11 .- ) \(\displaystyle \int \frac{dx}{\sqrt{a^2-x^2}}=\arctan \left(\frac{x}{a}\right)+C\)

12 .- ) \(\displaystyle \int \frac{dx}{x^2 \pm a^2 }= \ln \left|x+\sqrt{x^2\pm a^2}\right|+C\)

13 .- ) \(\displaystyle \int \frac{dx}{x(a+bx)}=\frac{1}{a} \ln \left| \frac{x}{a+bx} \right|+C\)

14 .- ) \(\displaystyle \int \frac{dx}{x^2(a+bx)}= -\frac{1}{ax} +\frac{b}{a^2}\ln \left| \frac{a+bx}{x} \right|+C\)

15 .- ) \(\displaystyle \int \frac{dx}{x(a+bx)^2}= \frac{1}{a+bx} - \frac{1}{a^2}\ln \left| \frac{a+bx}{x} \right|+C\)

16 .- ) \(\displaystyle \int x \sqrt{a+bx}, dx = \frac{2(3bx-2a)\sqrt{(a+bx)^3} }{15b^2}+C\)

17 .- ) \(\displaystyle \int \frac{x, dx}{\sqrt{a+bx} }=\frac{ 2(bx-2a)\sqrt{a+bx} }{3b^2}+C\)

18 .- ) \(\displaystyle \int x^2 \sqrt{a+bx}, dx = \frac{2(15b^2x^2-12abx+8a^2)\sqrt{(a+bx)^3} }{105b^3}+C\)

19 .- ) \(\displaystyle \int \frac{x^2, dx}{\sqrt{a+bx} }=\frac{ 2(3b^2x^2-4abx+8a^2)\sqrt{a+bx} }{15b^3}+C\)

20 .- ) \(\displaystyle \int \frac{dx}{x\sqrt{a+bx}}=\frac{1}{\sqrt a} \ln\left( \frac{\sqrt{a+bx}-\sqrt a}{\sqrt{a+bx}+\sqrt a}\right) + C \qquad \text{ if } a>0\)

21 .- ) \(\displaystyle \int \frac{dx}{x\sqrt{a+bx}}=\frac{2}{\sqrt{-a}} \arctan \sqrt{\frac{a+bx}{-a}} + C \qquad \text{ if } a<0\)

22 .- ) \(\displaystyle \int \frac{a+bx}{x}, dx = 2\sqrt{a+bx}+\int \frac{dx}{x\sqrt{a+bx}} + C\)

23 .- ) \(\displaystyle \int \frac{dx}{x^2\sqrt{a+bx}}=-\frac{\sqrt{a+bx}}{ax}-\frac{b}{2a}\int \frac{dx}{x\sqrt{a+bx}} + C\)

24 .- ) \(\displaystyle \int \sqrt{a^2-x^2}, dx = \frac{1}{2}\left(x\sqrt{a^2-x^2}+a^2\arctan\left(\frac{x}{a}\right)\right) + C\)

25 .- ) \(\displaystyle \int x\sqrt{a^2-x^2}, dx = -\frac{1}{3}(a^2-x^2)^{3/2} + C\)

26 .- ) \(\displaystyle \int x^2 \sqrt{a^2-x^2}, dx = \frac{x}{8}(2x^2-a^2)\sqrt{a^2-x^2}+\frac{a^4}{8}\arctan\left(\frac{x}{a}\right) + C\)

27 .- ) \(\displaystyle \int \frac{x, dx}{a^2-x^2} = -\sqrt{a^2-x^2} + C\)

28 .- ) \(\displaystyle \int \frac{x^2, dx}{a^2-x^2} = -\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}\arctan\left(\frac{x}{a}\right) + C\)

29 .- ) \(\displaystyle \int (a^2-x^2)^{3/2}, dx = \frac{x}{8}(5a^2-2x^2)\sqrt{a^2-x^2}+\frac{3a^4}{8}\arctan\left(\frac{x}{a}\right)+ C\)

30 .- ) \(\displaystyle \int \frac{dx}{(a^2-x^2)^{3/2}} = \frac{x}{a^2\sqrt{a^2-x^2}} + C\)

31 .- ) \(\displaystyle \int \frac{x, dx}{(a^2-x^2)^{3/2}} = \frac{1}{\sqrt{a^2-x^2}} + C\)

32 .- ) \(\displaystyle \int \frac{x^2, dx}{(a^2-x^2)^{3/2}} = \frac{x}{\sqrt{a^2-x^2}}-\arctan\left( \frac{x}{a}\right) + C\)

33 .- ) \(\displaystyle \int \frac{dx}{ x\sqrt{a^2-x^2} } = \frac{1}{a}\ln \left| \frac{a-\sqrt{a^2-x^2}}{x} \right| + C\)

34 .- ) \(\displaystyle \int \frac{dx}{x^2\sqrt{a^2-x^2}} = -\frac{\sqrt{a^2-x^2}}{a^2x} + C\)

35 .- ) \(\displaystyle \int \frac{dx}{x^3\sqrt{a^2-x^2}}=-\frac{\sqrt{a^2-x^2}}{2a^2x^2}+\frac{1}{2a^3}\ln\left|\frac{a-\sqrt{a^2-x^2}}{x} \right| + C\)

36 .- ) \(\displaystyle \int \frac{\sqrt{a^2-x^2}}{x}, dx = \sqrt{a^2-x^2}-a\ln \left| \frac{a+\sqrt{a^2-x^2}}{x} \right| + C\)

37 .- ) \(\displaystyle \int \frac{\sqrt{a^2-x^2}}{x^2}, dx =-\frac{\sqrt{a^2-x^2}}{x}-\arctan\left(\frac{x}{a}\right) + C\)

38 .- ) \(\displaystyle \int \sqrt{x^2 \pm a^2}, dx = \frac{1}{2}\left(x\sqrt{x^2 \pm a^2} \pm a^2\ln | x+\sqrt{x^2 \pm a^2} |\right) + C\)

39 .- ) \(\displaystyle \int x\sqrt{x^2 \pm a^2}, dx = \frac{1}{3} (x^2\pm a^2)^{3/2} + C\)

40 .- ) \(\displaystyle \int x^2\sqrt{x^2 \pm a^2}, dx = \frac{x}{8} (2x^2\pm a^2)\sqrt{x^2\pm a^2} -\frac{a^4}{8}\ln | x+\sqrt{x^2 \pm a^2} | + C\)

41 .- ) \(\displaystyle \int \frac{x, dx}{\sqrt{x^2\pm a^2}} = \sqrt{x^2 \pm a^2} + C\)

42 .- ) \(\displaystyle \int \frac{x^2 , dx}{\sqrt{x^2\pm a^2}} = \frac{1}{2} \left(x\sqrt{x^2 \pm a^2} \mp a^2\ln | x+\sqrt{x^2 \pm a^2} |\right)+ C\)

43 .- ) \(\displaystyle \int (x^2 \pm a^2)^{3/2} , dx = \frac{x}{8}(2x^2\pm 5a^2)\sqrt{x^2 \pm a^2} +\frac{3a^4}{8} \ln | x+\sqrt{x^2 \pm a^2} | + C\)

44 .- ) \(\displaystyle \int \frac{dx}{(x^2\pm a^2)^{3/2}} = \frac{\pm x}{a^2 \sqrt{x^2 \pm a^2}} + C\)

45 .- ) \(\displaystyle \int \frac{x, dx}{(x^2\pm a^2)^{3/2}} = \frac{-1}{ \sqrt{x^2 \pm a^2}} + C\)

46 .- ) \(\displaystyle \int \frac{x^2, dx}{(x^2\pm a^2)^{3/2}} = \frac{-x}{ \sqrt{x^2 \pm a^2}} + \ln | x+\sqrt{x^2 \pm a^2} |C\)

47 .- ) \(\displaystyle \int \frac{dx}{ x^2\sqrt{x^2 \pm a^2} } = \mp \frac{\sqrt{x^2 \pm a^2}}{a^2 x} + C\)

48 .- ) \(\displaystyle \int \frac{dx}{x^3 \sqrt{x^2 - a^2}} = \frac{ \sqrt{x^2-a^2}}{2a^2x^2}+\frac{1}{2a^3} \arccos\left(\frac{a}{x} \right) + C\)

49 .- ) \(\displaystyle \int \frac{\sqrt{x^2-a^2}}{x} , dx = \sqrt{x^2-a^2}-\arccos\left( \frac{a}{x} \right) + C\)

50 .- ) \(\displaystyle \int \frac{\sqrt{x^2\pm a^2}}{x^2}, dx = -\frac{\sqrt{x^2 \pm a^2}}{x}+\ln | x+\sqrt{x^2 \pm a^2} | + C\)

51 .- ) \(\displaystyle \int \frac{dx}{x\sqrt{x^2+a^2}} = \frac{1}{a} \ln \left|\frac{x}{a+\sqrt{x^2+a^2}} \right| + C\)

52 .- ) \(\displaystyle \int \frac{dx}{x\sqrt{x^2-a^2}} = \frac{1}{a}\arccos\left( \frac{a}{x} \right) + C\)

53 .- ) \(\displaystyle \int \frac{dx}{x^3\sqrt{x^2+a^2}}=-\frac{\sqrt{x^2+a^2}}{2a^2x^2}+\frac{1}{2a^3}\ln \left|\frac{a+\sqrt{x^2+a^2}}{x} \right| + C\)

54 .- ) \(\displaystyle \int \frac{x^2+a^2}{x}, dx = \sqrt{x^2+a^2}-a\ln \left| \frac{a+\sqrt{x^2+a^2}}{x}\right| + C\)

55 .- ) \(\displaystyle \int \sqrt{2ax-x^2}, dx = \frac{x-a}{2}\sqrt{2ax-x^2}+\frac{a^2}{2}\arctan \left(\frac{x-a}{a}\right) + C\)

56 .- ) \(\displaystyle \int \frac{dx}{\sqrt{2ax-x^2}} = 2\arctan\sqrt{\frac{x}{2a}} + C=\arccos\left(1-\frac{x}{a} \right)+C\)

57 .- ) \(\displaystyle \int \frac{x^n , dx}{\sqrt{2ax-x^2}} = -\frac{x^{n-1}\sqrt{2ax-x^2}}{n}+\frac{a(2n-1)}{n}\int \frac{ x^{n-1}, dx}{\sqrt{2ax-x^2}} + C\)

58 .- ) \(\displaystyle \int x^n\sqrt{2ax-x^2}, dx= \frac{\sqrt{2ax- x^2}}{a(1-2n)x^n}+\frac{n-1}{(2n-1)a}\int \frac{dx}{x^{n-1}\sqrt{2ax-x^2}}+ C\)

59 .- ) \(\displaystyle \int x^n\sqrt{2ax-x^2}, dx = -\frac{x^{n-1}(2ax-x^2)^{3/2}}{n+2}+\frac{(2n+1)a}{n+2} \int x^{n-1}\sqrt{2ax-x^2}, dx + C\)

60 .- ) \(\displaystyle \int \frac{ \sqrt{2ax-x^2}}{x^n} , dx = \frac{(2ax-x^2)^{3/2}}{(3-2n)ax^n}+\frac{n-3}{(2n-3)a} + C\)

61 .- ) \(\displaystyle \int \frac{dx}{ \sqrt{2ax-x^2}^{3/2} } = \frac{x-a}{ a^2 \sqrt{2ax-x^2} } + C\)

62 .- ) \(\displaystyle \int \frac{dx}{\sqrt{2ax+x^2}}=\ln | x+a+\sqrt{2ax+x^2}| + C\)

63 .- ) \(\displaystyle \int \frac{dx}{a+bx+cx^2}=\frac{2}{4ac-b^2}\arctan\left( \frac{2cx+b}{\sqrt{4ac-b^2}}\right) + C\)

64 .- ) \(\displaystyle \int \frac{dx}{a+bx-cx^2}=\frac{1}{\sqrt c},\arctan \left( \frac{2cx-b}{\sqrt{b+4ac}} \right) + C\)

65 .- ) \(\displaystyle \int \frac{dx}{a+bx-cx^2}=\frac{1}{b^2+4ac}, \ln \left| \frac{ \sqrt{b^2+4ac}-b+2cx}{\sqrt{b^2+4ac}+b-2cx} \right| + C\)

66 .- ) \(\displaystyle \int \frac{dx}{\sqrt{a+bx+cx^2}} = \frac{1}{\sqrt{c}}\ln |2cx+b+2\sqrt{c}\sqrt{a+bx+cx^2} | + C\)

67 .- ) \(\displaystyle \int \sqrt{a+bx+cx^2}, dx = \frac{2cx+b}{4c}\sqrt{a+bx+cx^2}) \[= -\frac{b^2-4ac}{8x^{3/2}} \ln |2cx+b+2\sqrt{c}\sqrt{a+bx+cx^2} | + C\]

68 .- ) \(\displaystyle \int \sqrt{a+bx-cx^2}, dx = \frac{2xc-b}{4c} \sqrt{a+bx-cx^2}+\frac{b^2+4ac}{8c^{3/2}} \arctan \left(\frac{2cx-b}{\sqrt{b^2+4ac}} \right)+ C\)

69 .- ) \(\displaystyle \int \frac{x, dx}{\sqrt{a+bx-cx^2}} = -\frac{\sqrt{a+bx-cx^2}}{c}+\frac{b}{2c^{3/2}},\arctan \left(\frac{2cx-b}{\sqrt{b^2+4ac}}\right) + C\)

70 .- ) \(\displaystyle \int \frac{x, dx}{\sqrt{a+bx+cx^2}} = \frac{\sqrt{a+bx+cx^2}}{c}- \frac{b}{2c^{3/2}} \ln |2cx+b+2\sqrt{c}\sqrt{a+bx+cx^2} | + C\)

71 .- ) \(\displaystyle \int \sin^2 (ax) , dx = \frac{1}{2a}(ax-\sin (ax)\cos(ax)) + C\)

72 .- ) \(\displaystyle \int \cos^2(ax), dx = \frac{1}{2a}(ax+\sin (ax)\cos (ax)) + C\)

73 .- ) \(\displaystyle \int \sin^n x, dx = -\frac{\sin^{n-1}x \cos x}{n}+\frac{n-1}{n}\int \sin^{n-2} x, dx + C\)

74 .- ) \(\displaystyle \int \cos^n x, dx = \frac{\cos^{n-1} x \sin x}{n}+\frac{n-1}{n} \int \cos^{n-2} x, dx+ C\)

75 .- ) \(\displaystyle \int \tan^n x, dx =\frac{\tan^{n-1} x}{n-1}-\int \tan{n-2}x, dx + C\)

76 .- ) \(\displaystyle \int \cot^n x, dx =\frac{\cot^{n-1} x}{n-1}-\int \cot^{n-2}x, dx + C\)

77 .- ) \( \displaystyle \int \sec^2 x, dx = \tan x + C\)

78 .- ) \( \displaystyle \int \csc^2 x, dx = -\cot x + C\)

79 .- ) \( \displaystyle \int \sec^n x, dx = \frac{\tan x \sec^{n-2} x}{n-1}+\frac{n-2}{n-1} \int \sec^{n-2} x, dx + C\)

80 .- ) \( \displaystyle \int \csc^n x , dx = -\frac{\cot x \csc^{n-2} x}{n-1} +\frac{n-2}{n-1} \int \csc^{n-2} x, dx + C\)

81 .- ) \( \displaystyle \int \sec x \tan x , dx = \sec x + C\)

82 .- ) \( \displaystyle \int \csc x \cot x = -\csc x + C\)

83 .- ) \( \displaystyle \int \cos^n x \sin^m x, dx = + C\) \[ = \frac{ \cos^{m-1} x \sin^{n+1} x }{m+n} + \frac{m-1}{m+n} \int \cos^{m-2} x \sin^n x , dx\] \[ = \frac{ \sin^{n-1} x \cos^{m+1} x }{m+n} + \frac{n-1}{m+n} \int \cos^{m} x \sin^{n-2} x , dx \] \[ = \frac{ \cos^{m+1} x \sin^{n+1} x }{m+1} + \frac{m+n+2}{m+1} \int \cos^{m+2} x \sin^n x , dx\] \[ = \frac{ \cos^{m+1} x \sin^{n+1} x }{n+1} + \frac{m+n+2}{n+1} \int \cos^{m} x \sin^{n+2} x , dx\]

Related Posts:

reset password

sign up